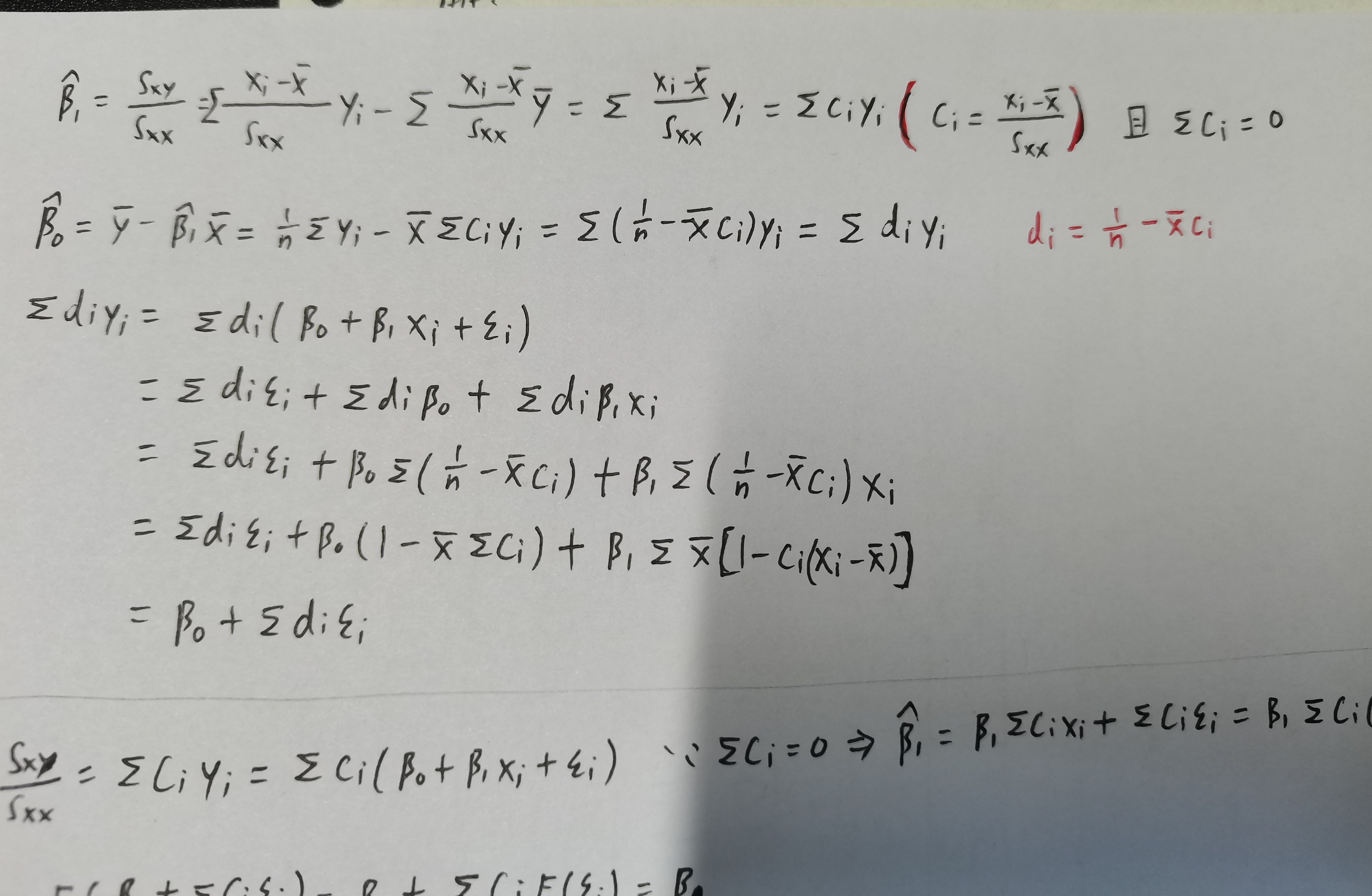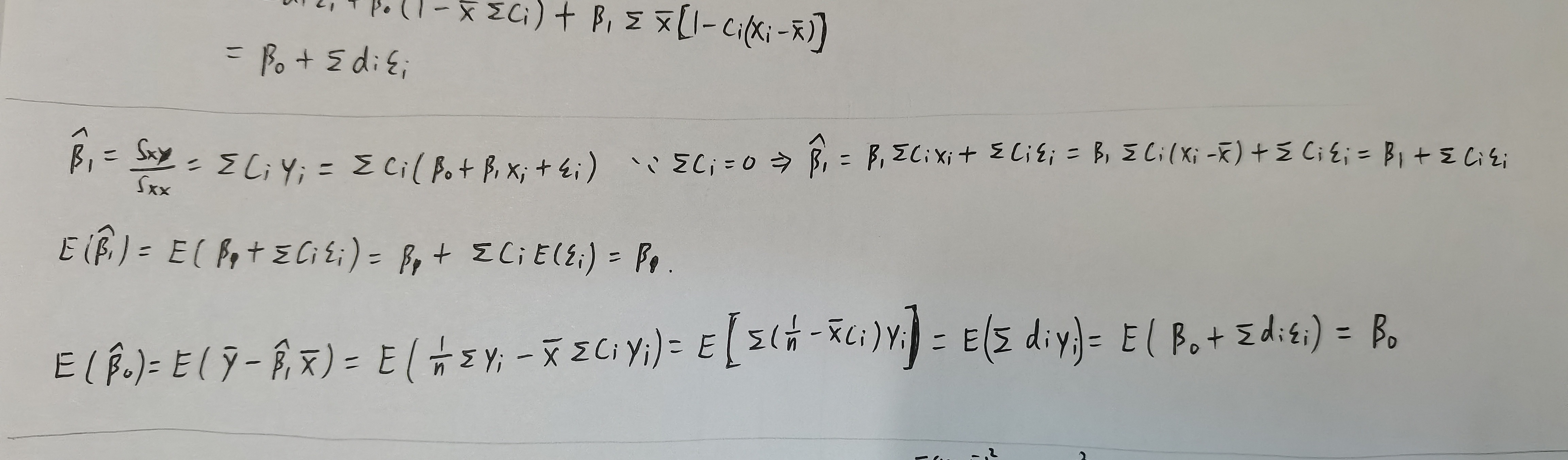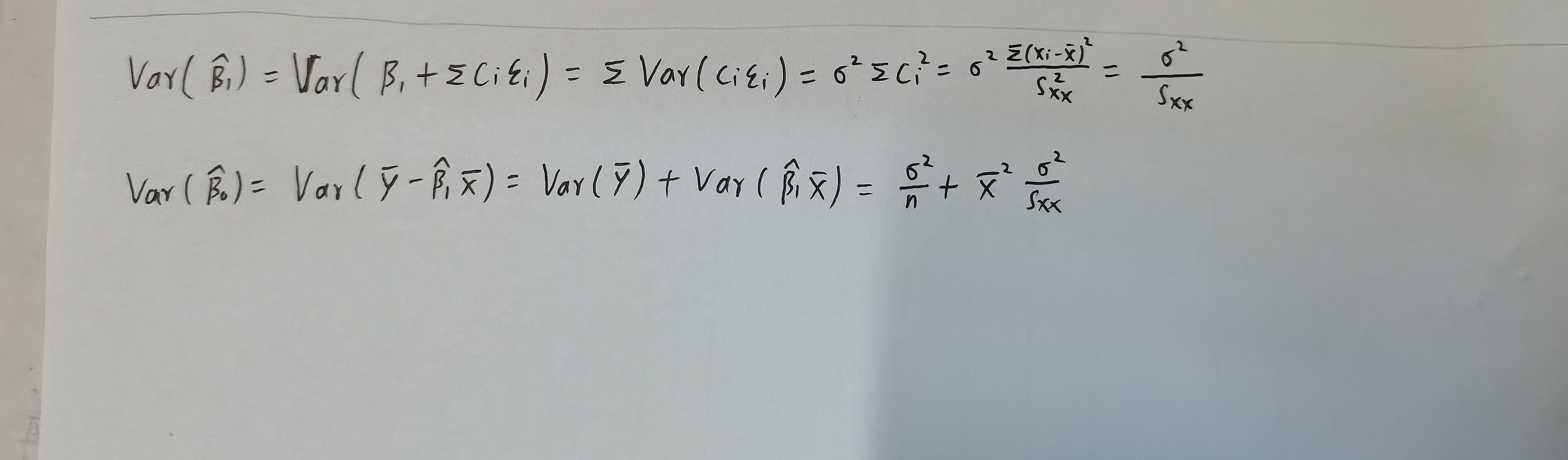回归分析-2.X 简单线性回归

2.1

简单线性回归模型

y与x之间的关系假设

\(y=\beta_0+\beta_1x+\varepsilon\)

\(E(\varepsilon|x)=0\)

\(Var(\varepsilon|x)=\sigma^2~则~Var(y|x)=\sigma^2\) 同方差假定

2.2

回归参数的最小二乘估计

回归系数 \(\beta_0,~\beta_1\) 的估计

残差平方和

\[S(\hat{\beta}_0,\hat{\beta}_1)=\sum^n_{i=1}(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)^2
\]

分别求偏导得到

\[\hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1} \bar{x}
\]

\[\hat{\beta}_{1}=\frac{\sum_{i=1}^{n} x_{i} y_{i}-n \cdot \bar{x} \cdot \bar{y}}{\sum_{i=1}^{n} x_{i}^{2}-n \cdot \bar{x}^{2}}=\frac{\sum\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum\left(x_{i}-\bar{x}\right)^{2}}=\frac{S_{x y}}{S_{x x}}
\]

性质

\[\frac{\partial S}{\partial\beta_0}=\sum(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)=0~\Rightarrow~\sum e_i=0
\]

\[\frac{\partial S}{\partial\beta_1}=\sum(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)x_i=0~\Rightarrow
\]

\[\sum e_ix_i=\sum (e_i-\bar{e})x_i=\sum(e_i-\bar{e})(x_i-\bar{x})=0
\]

进而知道\(\{e_i\}与\{x_i\}\) 互不相关

\(\sum(e_i-\bar{e})(y_i-\bar{y})=\sum e_iy_i=\sum e_i(\hat{\beta}_0+\hat{\beta}_1x_i)=\hat{\beta}_0\sum e_i+\hat{\beta}_1\sum(e_ix_i)=0\)

因此得出\(\{e_i\}与\{y_i\}\) 互不相关

\(\{e_i\}与\{\hat{y}_i\}\) 互不相关

\(Cov(\bar{y},\hat{\beta}_1)=0\)

\[\begin{aligned}
Cov(\bar{y},\hat{\beta}_1)&=\frac{1}{n}\sum Cov(y_i,\hat{\beta}_1)\\
&=\frac{1}{n}Cov(\sum y_i,\sum c_iy_i)\\
&=\frac{1}{n}\sum (c_i\sigma^2)\\
&=0
\end{aligned}\]

• OLS是线性估计
  
  

• OLS是无偏估计
  
  

• LS估计的方差可计算为
  
  

随机误差方差的 \(\sigma^2\) 估计

均方误差

\[\begin{array} aMSE(\theta)=E(\hat{\theta}-\theta)^2=E(\hat{\theta}-E(\hat{\theta})+E(\hat{\theta})-\theta)^2=Var(\hat{\theta})+(bias(\hat{\theta}))^2\\
bias(\hat{\theta})=E(\hat{\theta})-\theta\end{array}\]

定义

\[S S_{\text {Res }}=\sum_{i=1}^{n} e_{i}^{2}=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}=\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{i}\right)^{2}
\]

\[\hat{\sigma}^{2}=\frac{S S_{\text {Res }}}{n-2}=M S_{\text {Res }}
\]

在第三章我们将证明 \(E\left(\hat{\sigma}^{2}\right)=\sigma^{2}\)

参数估计的标准误

\[s.e.(\hat{\beta}_1)=\sqrt{\frac{\frac{S S_{\text {res }}}{n-2}}{S_{xx}}}
\]

\[s.e.(\hat{\beta}_0)=\sqrt{\frac{\frac{S S_{\text {res }}}{n-2}}{n}+\bar{x}^2\frac{\frac{S S_{\text {res }}}{n-2}}{S_{xx}}}
\]

2.3

斜率与截距的假设检验

OLS 估计的抽样分布

\[\hat{\beta}_{1}=\sum_{i=1}^{n} c_{i} y_{i}=\beta_{1}+\sum_{i=1}^{n} c_{i} \epsilon_{i}, \quad \hat{\beta}_{0}=\sum_{i=1}^{n} d_{i} y_{i}=\beta_{0}+\sum_{i=1}^{n} d_{i} \epsilon_{i}
\]

\[\hat{\beta}_{1}\sim N(\beta_1,\frac{\sigma^2}{S_{xx}})~,~ ~ \hat{\beta}_{0}\sim N(\beta_0,\bar{x}^2\frac{\sigma^2}{S_{xx}})
\]

t 检验

由于

\[t_{0}=\frac{\hat{\beta}_{1}-\beta_{10}}{\hat{\sigma} / \sqrt{S_{x x}}}=\frac{\hat{\beta}_{1}-\beta_{10}}{\hat{\sigma} / \sqrt{S_{x x}}} \frac{\sigma}{\hat{\sigma}}=\frac{Z_{0}}{\sqrt{\frac{SS_{\text {res }}}{(n-2) \sigma^{2}}}}=Z_{0} / \sqrt{\frac{M S_{\text {res }}}{\sigma^{2}}} \sim t(n-2)
\]

因此,为了检验两变量间是否有线性关系,将假设斜率 \(\beta_{10}=0\)

t检验统计量为

\[t=\frac{\hat{\beta}_1}{\hat{\sigma}/\sqrt{S_{xx}}}=\frac{\hat{\beta}_1}{s.e.(\hat{\beta}_1)}={\hat{\beta}_1}/{\sqrt{\frac{\frac{S S_{\text {res }}}{n-2}}{S_{xx}}}}
\]

p 值

\[pvalue=P(|t_{n-2}|>|\frac{\hat{\beta}_1}{s.e.(\hat{\beta}_1)}|)
\]

区间估计

参数的置信区间

\(\beta_0~\beta_1\)的置信区间

\[\frac{\hat{\beta}_{1}-\beta_{1}}{s . e .\left(\hat{\beta}_{1}\right)} \sim t({n-2}), \quad \frac{\hat{\beta}_{0}-\beta_{0}}{s . e .\left(\hat{\beta}_{0}\right)} \sim t({n-2})
\]

可得 \(\beta_{i}\) 的 \(1-\alpha\) 置信区间为

\[\hat{\beta}_{i} \pm t_{n-2}(1-\alpha / 2) * \text { s.e. }\left(\hat{\beta}_{i}\right)
\]

响应变量均值 \(E(y|x_0)\) 的估计和置信区间

\(\because\)

\(E\left(y \mid x_{0}\right)=\beta_{0}+\beta_{1} x_{0}\)

\(\therefore\)

\(\hat{\mu}_{y \mid x_{0}}=\hat{\beta}_{0}+\hat{\beta}_{1} x_{0}=\bar{y}+\hat{\beta}_{1}\left(x_{0}-\bar{x}\right)\)

而且

\[Var\left(y \mid x_{0}\right)=\sigma^2({\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}})
\]

可知

\[\frac{\hat{\mu}_{y \mid x_{0}}-\mu_{y \mid x_{0}}}{\hat{\sigma} \sqrt{\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}} \sim t({n-2})
\]

所以\(E(y|x_0)\) 的置信区间

\[\hat{\mu}_{y \mid x_{0}}\pm t_{n-2}(1-\alpha/2)\hat{\sigma} \sqrt{\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}
\]

新观测的预测

预测误差为

\[\begin{aligned}\psi&=y_{0}-\hat{y}_{0}\\
&=\beta_{0}+\beta_{1} x_{0}+\epsilon_{0}-(\hat{\beta}_{0}+\hat{\beta}_{1} x_{0})\\
&=(\beta_{0}-\hat{\beta}_{0})+(\beta_{1}-\hat{\beta}_{1}) x_{0}+\epsilon_{0}
\end{aligned}\]

预测方差为

\[\begin{aligned}\operatorname{Var}(\psi)&=\operatorname{Var}(y_{0}-\hat{y}_{0})\\
&=\operatorname{Var}(\hat{\beta}_{0}+\hat{\beta}_{1} x_{0}+\epsilon_{0})\\
&=\sigma^2(1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}})
\end{aligned}\]

因此有

\[\frac{\psi-E(\psi)}{\sqrt{\operatorname{Var}(\psi)}}=\frac{y_{0}-\hat{y}_{0}}{\sigma \sqrt{1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}} \sim N(0,1)
\]

所以

\[\frac{y_{0}-\hat{y}_{0}}{\hat{\sigma} \sqrt{1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}} \sim t_{n-2}
\]

于是可得 \(1-\alpha\) 预测区间为

\[\hat{y}_{0} \pm t_{n-2}(1-\alpha / 2) \hat{\sigma} \sqrt{1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}
\]

决定系数 \(R^2\)

可以定义

\[\begin{aligned}
S S_{\text {total }}&=\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}\\
&=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}+\hat{y}_{i}-\bar{y}\right)^{2}\\
&=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}+\sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}\right)^{2}+2 \sum_{i=1}^{n} e_{i}\left(\hat{y}_{i}-\bar{y}\right) \triangleq \text { SSres }+\text { SSreg }
\end{aligned}\]

\[R^{2}=\frac{SS_{reg}}{SS_T}=\frac{S S_{t o t a l}-S S_{r e s}}{S S_{t o t a l}}
\]

表明了 y 的样本变异中被 x 解释了的部分

可以推导出下列结论

\[R^{2}=\frac{\hat{\beta}_{1}^{2}}{\hat{\beta}_{1}^{2}+\frac{n-2}{n-1} \cdot \frac{\hat{\sigma}^{2}}{\hat{\sigma}_{x}^{2}}}
\]

因此 \(R^{2}\) 较大, 并不意味着斜率 \(\hat{\beta}_{1}\) 就较大;

• 应该谨慎地解释和使用 \(R^{2}\) 。在实际问题里, \(R^{2}\) 作为模型拟合优 度的度量是有缺陷的, 一个典型的问题是, 在多元线性回归模型 里, 加人一个变量总会使得 \(R^{2}\) 升高, 因此用它做标准选择模型 的话, 总是会选取一个最复杂的模型。
• 若 \(R^{2}=1\) ,则完美拟合
• 若 \(R^{2}=0\) ,则两变量无关系