6.20 NOI 模拟
\(T1\ left\ xor\ right\)
考虑把询问离线，查询变成 \([0,x-1]\) 的 \([l,r]\) 的区间和与 \([0,y]\) 的 \([l,r]\) 的区间和的差
考虑线段树维护矩阵
\begin{array}{ccc}
\displaystyle\sum_{i=l}^r a_i & \displaystyle\sum_{i=l}^r a_i^2 & r-l+1 & \displaystyle\sum_{x} \sum_{i=l}^r a_i^2 \\
\end{array}
\right]
\]
对于区间加 \(k\) 维护 \(lz\) 矩阵
\begin{array}{ccc}
1 & 2\times k & 0 & 2\times k
\\
0 & 1 & 0 & 1
\\
k & k^2 & 1 & k^2
\\
0 & 0 & 0 & k
\end{array}
\right]
\]
#define Eternal_Battle ZXK
#include<bits/stdc++.h>
#define rs ((now<<1)|1)
#define int long long
#define ls (now<<1)
#define MAXN 50005
using namespace std;
const int mod=1000000007;
int n,m,q;
struct Md
{
int l,r,v;
}md[MAXN];
struct Que
{
int l,r,opt,id;
};
vector<Que>que[MAXN];
struct Mat
{
int jz[5][5];
void st()
{
memset(jz,0,sizeof(jz));
for(int i=1;i<=4;i++) jz[i][i]=1;
}
void Init()
{
memset(jz,0,sizeof(jz));
}
}tag;
struct node
{
int l,r;
bool flag;
Mat mes,lz;
}tr[MAXN<<2];
int a[MAXN],Ans[MAXN];
void push_up(int now)
{
tr[now].mes.jz[1][1]=(tr[ls].mes.jz[1][1]+tr[rs].mes.jz[1][1])%mod;
tr[now].mes.jz[1][2]=(tr[ls].mes.jz[1][2]+tr[rs].mes.jz[1][2])%mod;
tr[now].mes.jz[1][3]=(tr[ls].mes.jz[1][3]+tr[rs].mes.jz[1][3])%mod;
tr[now].mes.jz[1][4]=(tr[ls].mes.jz[1][4]+tr[rs].mes.jz[1][4])%mod;
}
void build(int now,int l,int r)
{
tr[now].l=l,tr[now].r=r;
tr[now].lz.st();
if(l==r)
{
tr[now].mes.jz[1][1]=a[l];
tr[now].mes.jz[1][2]=a[l]*a[l]%mod;
tr[now].mes.jz[1][3]=1;
tr[now].mes.jz[1][4]=a[l]*a[l]%mod;
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
push_up(now);
}
Mat mul(Mat a,Mat b)
{
Mat res;
res.Init();
for(int i=1;i<=4;i++)
{
for(int j=1;j<=4;j++)
{
for(int k=1;k<=4;k++)
{
res.jz[i][j]=(res.jz[i][j]+a.jz[i][k]*b.jz[k][j]%mod)%mod;
}
}
}
return res;
}
void pd(int now)
{
if(tr[now].flag==true)
{
Mat lz=tr[now].lz;
tr[ls].flag=true;
tr[ls].lz=mul(tr[ls].lz,lz);
tr[ls].mes=mul(tr[ls].mes,lz);
tr[rs].flag=true;
tr[rs].lz=mul(tr[rs].lz,lz);
tr[rs].mes=mul(tr[rs].mes,lz);
tr[now].lz.st();
tr[now].flag=false;
}
}
void change(int now,int l,int r)
{
if(tr[now].l>=l&&tr[now].r<=r)
{
tr[now].mes=mul(tr[now].mes,tag);
tr[now].lz=mul(tr[now].lz,tag);
tr[now].flag=true;
return ;
}
pd(now);
int mid=(tr[now].l+tr[now].r)>>1;
if(l<=mid) change(ls,l,r);
if(r>mid) change(rs,l,r);
push_up(now);
}
void Init(int k)
{
for(int i=1;i<=4;i++) tag.jz[i][i]=1;
tag.jz[1][2]=tag.jz[1][4]=2*k%mod;
tag.jz[2][4]=1;
tag.jz[3][1]=k; tag.jz[3][2]=k*k%mod; tag.jz[3][4]=k*k%mod;
}
int query(int now,int l,int r)
{
if(tr[now].l>=l&&tr[now].r<=r)
{
return tr[now].mes.jz[1][4];
}
pd(now);
int mid=(tr[now].l+tr[now].r)>>1;
int res=0;
if(l<=mid) res=(res+query(ls,l,r))%mod;
if(r>mid) res=(res+query(rs,l,r))%mod;
return res;
}
signed main()
{
scanf("%lld%lld%lld",&n,&m,&q);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=m;i++) scanf("%lld%lld%lld",&md[i].l,&md[i].r,&md[i].v);
for(int i=1,l,r,x,y;i<=q;i++)
{
scanf("%lld%lld%lld%lld",&l,&r,&x,&y);
if(x!=0)que[x-1].push_back((Que){l,r,-1,i});
que[y].push_back((Que){l,r,1,i});
}
build(1,1,n);
for(int i=0;i<que[0].size();i++)
{
int l=que[0][i].l,r=que[0][i].r,opt=que[0][i].opt,id=que[0][i].id;
(Ans[id]+=mod+opt*query(1,l,r)%mod)%=mod;
}
for(int i=1;i<=m;i++)
{
Init(md[i].v);
change(1,md[i].l,md[i].r);
if(md[i].l>1) Init(0),change(1,1,md[i].l-1);
if(md[i].r<n) Init(0),change(1,md[i].r+1,n);
for(int j=0;j<que[i].size();j++)
{
int l=que[i][j].l,r=que[i][j].r,opt=que[i][j].opt,id=que[i][j].id;
int res=query(1,l,r);
(Ans[id]+=(mod+opt*res%mod))%=mod;
}
}
for(int i=1;i<=q;i++)
{
cout<<Ans[i]<<"\n";
}
}
\(T2\ lots\ of\ valuable\ energy\)
先考虑我们可以指定一条路径使其成为直径，那么我们应该对这个直径进行最优化赋值
设我们能给这个子树丢弃的无用边数量为 \(b_i\)
转移易得
\rightarrow\left\{
\begin{array}{**lr**}
f(l-1,r,t+1)+a[t+1]\\
f(l,r+1,t+1)+a[t+1]\\
f(l,r,t+1)\ \ \ \displaystyle\sum_{i=l}^rb_i\leq t+1 \\
\end{array}
\right.
\]
这个的复杂度是 \(O(n^3)\)
考虑把 \(dp\) 过程转移到树上
设 \(dp[u][v][t][Sit],Sit=0/1/2/3\)
\(dp[u][v][t][0]\) 表示路径 \(u\rightarrow v\) 的最长距离，并且扩展结束
\(dp[u][v][t][1]\) 表示路径 \(u\rightarrow pre[v]\) 的最长距离，并且 \(u\) 扩展结束，下一步向 \(v\) 扩展，\(pre[v]\) 表示 \(u\rightarrow v\) 路径上 \(v\) 的前一个点
\(dp[u][v][t][2]\) 表示路径 \(pre[u]\rightarrow v\) 的最长距离，并且 \(v\) 扩展结束，下一步向 \(u\) 扩展
\(dp[u][v][t][3]\) 表示路径 \(pre[u]\rightarrow pre[v]\) 的最长距离，下一步向两侧 \(u,v\) 扩展
和上面的转移类似
其实为了省事，直接枚举 \(u,v\) 进行第一个转移就好，比较显然的只能选叶子，就可以很好地剪枝了(但是被未知原因卡掉了一个点就特判过去了)
#define Eternal_Battle ZXK
#include<bits/stdc++.h>
#define ll long long
#define MAXN 305
using namespace std;
int head[MAXN],nxt[MAXN],to[MAXN],b[MAXN],tot;
int siz[MAXN],sum[MAXN],pre[MAXN],cnt;
ll dp[MAXN][MAXN][MAXN],Ans;
int du[MAXN],a[MAXN],n;
bool vis[MAXN],flag;
void add(int u,int v)
{
tot++;
to[tot]=v;
nxt[tot]=head[u];
head[u]=tot;
}
void dfs_pre(int now,int fa,int ed)
{
vis[now]=true;
if(now==ed)
{
flag=true;
return ;
}
for(int i=head[now];i;i=nxt[i])
{
int y=to[i];
if(y==fa||flag) continue;
dfs_pre(y,now,ed);
}
if(!flag)vis[now]=false;
}
void dfs_siz(int now,int fa)
{
siz[now]=1;
for(int i=head[now];i;i=nxt[i])
{
int y=to[i];
if(y==fa) continue;
dfs_siz(y,now);
siz[now]+=siz[y];
if(vis[y]) sum[now]-=siz[y];
}
sum[now]+=siz[now];
if(vis[now]) b[++cnt]=sum[now];
}
int ss=0;
void sol(int u,int v)
{
memset(vis,0,sizeof(vis));
memset(sum,0,sizeof(sum));
flag=false;
cnt=0;
dfs_pre(u,u,v);
dfs_siz(u,u);
for(int i=1;i<=cnt;i++) pre[i]=pre[i-1]+b[i];//cout<<b[i]<<" ";
for(int i=1;i<=cnt;i++) for(int j=0;j<=b[i];j++) dp[i][i][j]=0;
for(int len=1;len<=cnt;len++)
{
for(int l=1;l+len-1<=cnt;l++)
{
int r=(l+len-1);
for(int t=len-1;t<=pre[r]-pre[l-1]+(r-l);t++)
{
if(l!=1) dp[l-1][r][t+1]=max(dp[l-1][r][t+1],dp[l][r][t]+a[t+1]);
if(r!=cnt) dp[l][r+1][t+1]=max(dp[l][r+1][t+1],dp[l][r][t]+a[t+1]);
dp[l][r][t+1]=max(dp[l][r][t],dp[l][r][t+1]);ss++;
}
}
}
ll res=0;
for(int i=cnt-1;i<=pre[cnt]+cnt-1;i++)
{
res=max(res,dp[1][cnt][i]);
}
Ans=max(Ans,res);
}
signed main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1,u,v;i<=n;i++) scanf("%d%d",&u,&v),add(u,v),add(v,u),du[u]++,du[v]++;
for(int u=1;u<=n+1;u++)
{
if(du[u]!=1) continue;
for(int v=u+1;v<=n+1;v++)
{
if(du[v]!=1) continue;
sol(u,v);
}
}
if(Ans==34) cout<<33<<"\n";
else cout<<Ans<<"\n";
}
\(T3\ young\ xanthous\ host\)
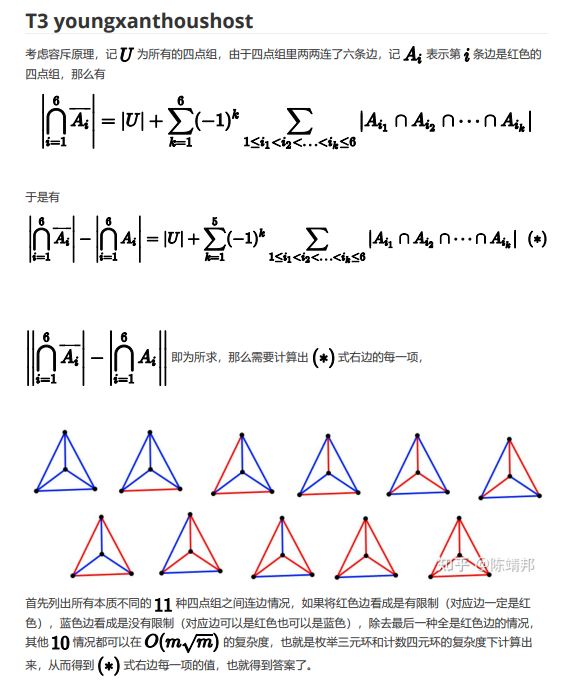
#include<bits/stdc++.h>
#define ll __int128
#define int long long
#define P make_pair
using namespace std;
const int N=100010,M=200010;
int n,m,deg[N],cnt[M],tag[N];
ll res,one;
int X[M],Y[M];
vector<pair<int,int> > road[N],h[N];
ll C(int n,int m)
{
if(n<m)return 0;
ll ret=1;
for(int i=0;i<m;++i) ret*=n-i;
for(int i=1;i<=m;++i) ret/=i;
return ret;
}
inline bool cmp(int x,int y)
{
if(deg[x]!=deg[y]) return deg[x]>deg[y];
else return x>y;
}
void print(ll x)
{
if(x/10) print(x/10);
putchar('0'+x%10);
}
signed main()
{
one=1;
scanf("%lld %lld",&n,&m);
for(int i=1;i<=m;++i)
{
scanf("%lld %lld",&X[i],&Y[i]);
road[X[i]].push_back(P(Y[i],i));
road[Y[i]].push_back(P(X[i],i));
deg[X[i]]++,deg[Y[i]]++;
}
for(int i=1;i<=m;++i)
if(P(deg[X[i]],X[i])>P(deg[Y[i]],Y[i])) h[X[i]].push_back({Y[i],i});
else h[Y[i]].push_back({X[i],i});
res=C(n,4)-one*m*C(n-2,2)+C(m,2);
for(int i=1;i<=n;++i) res+=one*C(deg[i],2)*(n-4)-C(deg[i],3);
for(int i=1;i<=m;++i) res-=one*(deg[X[i]]-1)*(deg[Y[i]]-1);
for(int x=1;x<=n;++x)
{
for(int i=0;i<road[x].size();++i) tag[road[x][i].first]=road[x][i].second;
for(int i=0;i<h[x].size();++i)
{
int v=h[x][i].first;
for(int j=0;j<h[v].size();++j)
{
int t=h[v][j].first;
if(!tag[t])continue;
res+=deg[x]+deg[v]+deg[t]-n;
cnt[h[x][i].second]++,cnt[h[v][j].second]++,cnt[tag[t]]++;
}
}
for(int i=0;i<road[x].size();++i) tag[road[x][i].first]=0;
}
for(int x=1;x<=n;++x)
{
for(int i=0;i<h[x].size();++i)
{
int v=h[x][i].first;
for(int j=0;j<road[v].size();++j)
{
int t=road[v][j].first;
if(!cmp(x,t))continue;
res+=tag[t];
tag[t]++;
}
}
for(int i=0;i<h[x].size();++i)
{
int v=h[x][i].first;
for(int j=0;j<road[v].size();++j)
tag[road[v][j].first]=0;
}
}
for(int i=1;i<=m;++i) res-=C(cnt[i],2);
print(res<0?-res:res);
}
6.20 NOI 模拟的更多相关文章
- 5.30 NOI 模拟
$5.30\ NOI $模拟 高三大哥最后一次模拟考了,祝他们好运 \(T1\)装箱游戏 显然可以将四种字母之间的空缺当做状态枚举 那么这道题就很显然了 #include<bits/stdc++ ...
- 5.23 NOI 模拟
$5.23\ NOI $模拟 \(T1\)简单的计算几何题 \(zjr:\)我当时没改,那么自己看题解吧 倒是有个简单的随机化方法(能获得\(72pts,\)正确性未知)\(:\) 随机两条切椭圆的平 ...
- 5.6 NOI模拟
\(5.6\ NOI\)模拟 明天就母亲节了,给家里打了个电话(\(lj\ hsez\)断我电话的电,在宿舍打不了,只能用教练手机打了) 其实我不是很能看到自己的\(future,\)甚至看不到高三的 ...
- 5.4 NOI模拟
\(5.4\ NOI\)模拟 \(T1\) 想到分讨,但是暴力输出一下方案之后有很多特别的情况要讨论,就弃了... 假设\(a\)是原序列,\(b\)是我们得到的序列 设\(i\)是最长公共前缀,\( ...
- 【2019.3.20】NOI模拟赛
题目 这里必须标记一下那个傻逼问题,再不解决我人就没了! 先放一个 $T3$ $20$ 分暴力 #include<bits/stdc++.h> #define rep(i,x,y) for ...
- NOI模拟赛 Day1
[考完试不想说话系列] 他们都会做呢QAQ 我毛线也不会呢QAQ 悲伤ING 考试问题: 1.感觉不是很清醒,有点困╯﹏╰ 2.为啥总不按照计划来!!! 3.脑洞在哪里 4.把模拟赛当作真正的比赛,紧 ...
- 9.20 noip模拟试题
Problem 1 双色球(ball.cpp/c/pas) [题目描述] 机房来了新一届的学弟学妹,邪恶的chenzeyu97发现一位学弟与他同名,于是他当起了善良的学长233 “来来来,学弟,我 ...
- 6.28 NOI模拟赛 好题 状压dp 随机化
算是一道比较新颖的题目 尽管好像是两年前的省选模拟赛题目.. 对于20%的分数 可以进行爆搜,对于另外20%的数据 因为k很小所以考虑上状压dp. 观察最后答案是一个连通块 从而可以发现这个连通块必然 ...
- NOI模拟赛Day5
T1 有and,xor,or三种操作,每个人手中一个数,求和左边进行某一种运算的最大值,当t==2时,还需要求最大值的个数. test1 20% n<=1000 O(n^2)暴力 test2 2 ...
随机推荐
- [C++STL] 队列 queue 的入门
队列结构 概念: 队列(queue):和栈相似,也是一种特殊的线性表.和栈不同的是,队列只允许在表的一端进行插入操作,而在另一端进行删除操作.一般来说,进行插入操作的一端称为队尾,进行删除操作的一端称 ...
- 安装Redis到Linux（源码）
运行环境 系统版本:Ubuntu 16.04.2 LTS 软件版本:redis-5.0.4 硬件要求:无 安装过程 1.配置系统参数 root@localhost:~# vim /etc/sysctl ...
- 什么！Sentinel流控规则可以这样玩？
项目源码地址:公众号回复 sentinel,即可免费获取源码 前言 上一篇文章中,我们讲解了关于sentinel基本介绍以及流控规则中直接和快速失败的效果,有兴趣的可以去看上一篇文章,今天,我们给大家 ...
- Pandas：添加修改、高级过滤
1.添加修改数据 Pandas 的数据修改是进行赋值,先把要修改的数据筛选出来,然后将同结构或者可解包的数据赋值给它: 修改数值 df.Q1 = [1, 3, 5, 7, 9] * 20 # 就会把值 ...
- 绿色城市智慧运营：Web 3D 垃圾分类 GIS 系统
前言 感谢所有为上海疫情奉献的人,祈求上海疫情早日清零,中国加油,上海加油! <上海市生活垃圾管理条例>施行至今已有两年多,上海市民践行绿色低碳理念.主动参与生活垃圾分类的习惯基本养成,分 ...
- Go微服务框架go-kratos实战02：proto 代码生成和编码实现步骤
在上一篇 kratos quickstart 文章中,我们直接用 kratos new 命令生成了一个项目. 这一篇来看看 kratos API 的定义和使用. 一.kratos 中 API 简介 1 ...
- 技术分享 | app测试中常用的Android模拟器
原文链接 Emulator Emualor 是 Android Studio 自带的模拟器,是官方提供的工具,Android 开发最常使用的就是这一款. 它功能非常齐全,电话本.通话等功能都可正常使用 ...
- 【2022-06-16】Python解释器的下载安装与使用
一.Python解释器介绍 什么是Python解释器? Python是一门解释型语言,解释器是Python运行必不可少的一种工具.所以,我们搭建Python环境,本质上就是对Python进行配置和定制 ...
- 皓远的第一次博客作业(pta题目集——1-3）
题目集总结: 前言: 一. 知识点运用: ① Java入门的基础语法(循环,判断,字符串,数组等等),Java的基础类运用,类与对象关系调用,类间关系(聚合). ② 引(类与对象): 对象 ...
- spring源码解析：元注解功能的实现
前言 众所周知,spring 从 2.5 版本以后开始支持使用注解代替繁琐的 xml 配置,到了 springboot 更是全面拥抱了注解式配置.平时在使用的时候,点开一些常见的等注解,会发现往往在一 ...