「学习笔记」斜率优化dp
算法
把一些 dp 的转移方程拆一拆,移一移,能拆成 \(y=kx+b\) 的形式(其中 \(k,b\) 只与当前的 \(i\) 有关,\(x,y\) 只与 \(j\) 有关,\(b\) 包含 \(f_i\))。
然后我们用单调队列维护一些点形成的凸包,每次找一个最优的点。
详见例题任务安排。
例题
任务安排
题意
有 \(N\) 个任务,每个任务都有一个所需时间 \(T_i\) 和费用 \(C_i\)。
现在要求你把这些任务分成若干批,每批任务所需费用为机器启动时间 \(S\) 加上这批任务的总时间再乘上这批任务的总费用。
求最小费用。
\(1 \le n \le 3 \times 10^5\),\(1 \le s \le 2^8\),\(0\le T_i \le 2^8\),\(0 \le C_i \le 2^8\)。
思路
转移方程为:
\]
咋算的?
设 \(f_i\) 表示把前 \(i\) 个任务划分成了若干段的最小费用,那么我们要找到一个 \(j\),使 \(f_j\) 加上 \((j+1,i)\) 这些任务的费用的总费用最小。
其中,\(SumT_i*(SumC_i-SumC_j)\) 是这些任务执行完的总费用,\(S*(SumC_n-SumC_j)\) 是这个启动时间对之后的所用任务产生的影响
拆一下可得:
\]
原式去掉 \(\min\) 得:
\]
进一步变形为:
\]
此时令:
x=SumC_j\\
y=f_j\\
k=(SumT_i+S)\\
b=f_i-SumT_i*SumC_i-S*SumC_n\\
\end{cases}
\]
则原转移方程就变成了一个直线方程 \(y=kx+b\)。
我们要让 \(f_i\) 尽量小,就是让截距 \(b\) 尽量小.
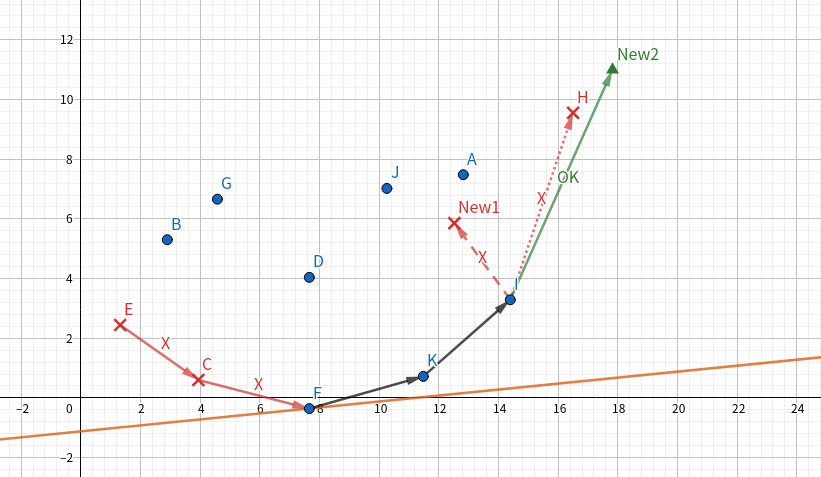
那么画一个横坐标 \(SumC_j\),纵坐标 \(f_j\) 的坐标系。
我们把 \((SumC_j,f_j)\ (1\le j<i)\) 这些点都放到坐标系上。
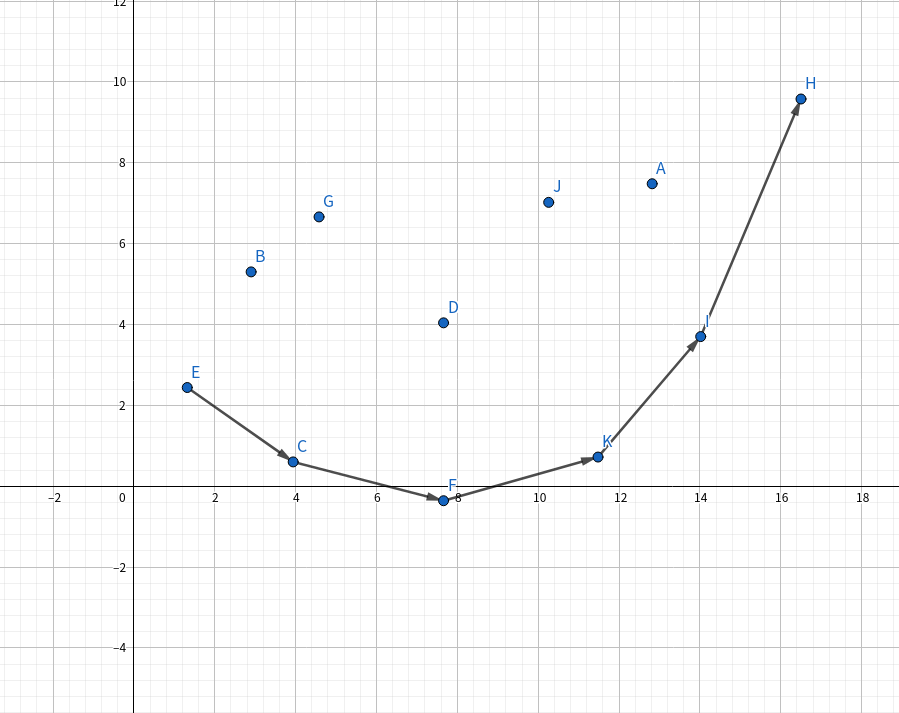
然后我们把直线 \(y=kx+b\) 放上去。
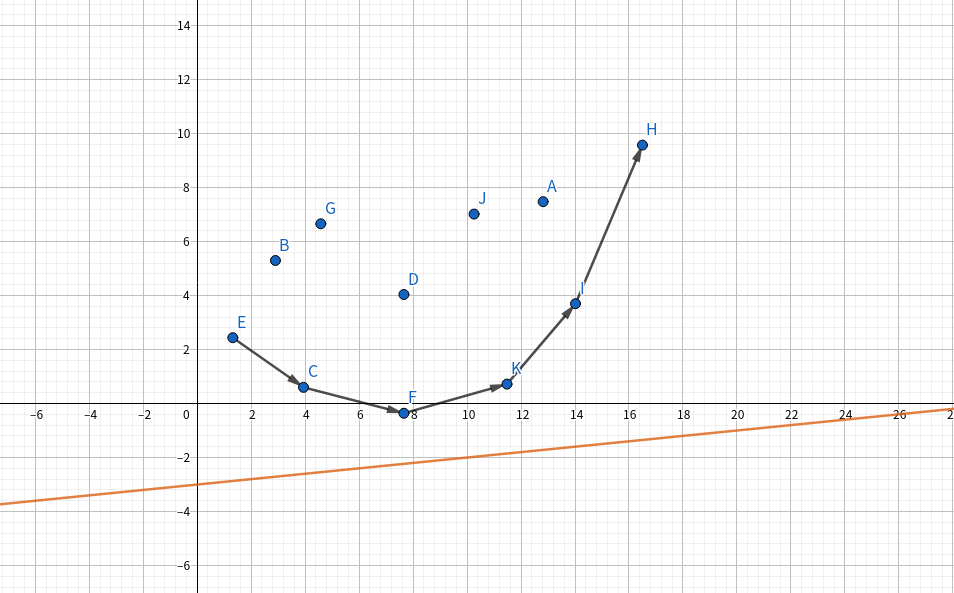
再往上移移移移移,看能碰到那个点,那个点就是我们想要的使 \(f_i\) 最小的点。
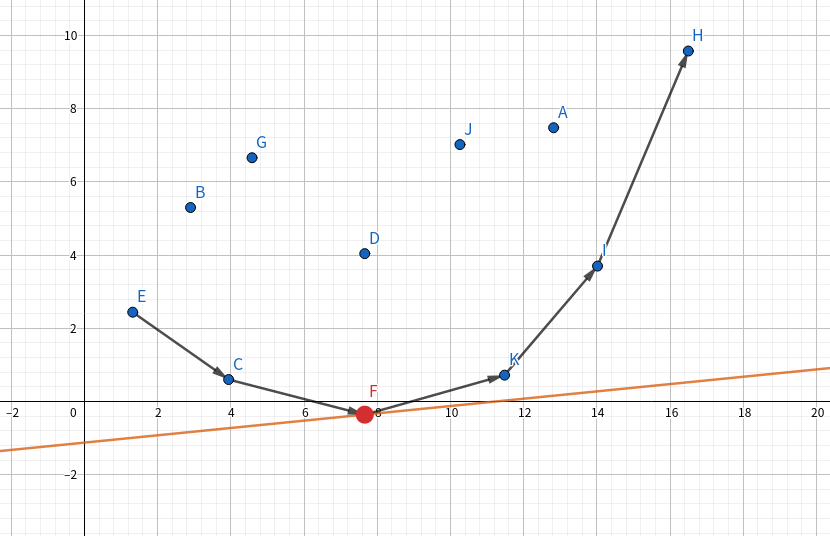
可以发现,有可能被碰上的点在一个下凸包上。
那么我们只要用单调队列维护这个相邻两点之间斜率递增的下凸包就可以了。
每加入一个点,都要保证这些点的斜率是递增的,即 \(\dfrac{f_{tail}-f_{tail-1}}{SumC_{tail}-SumC_{tail-1}}\ge\dfrac{f_{i}-f_{tail}}{Sum_{i}-SumC_{tail}}\)。
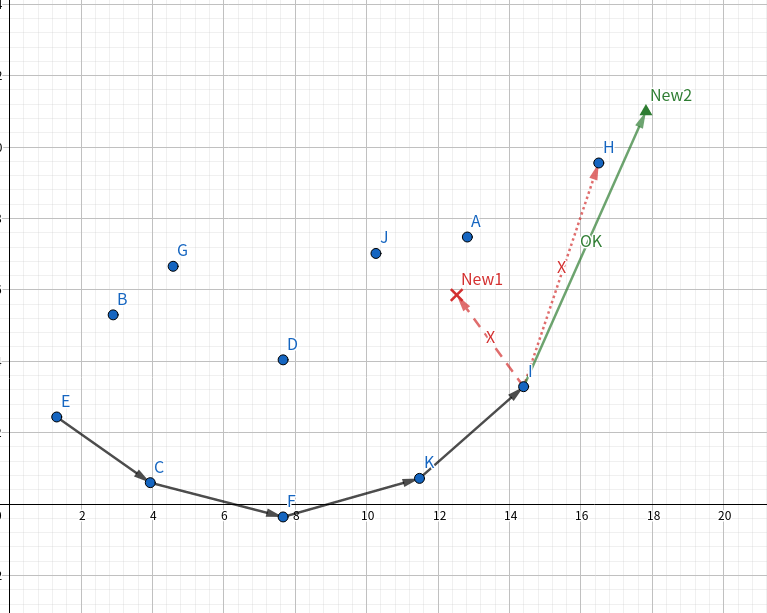
对于这道题,\(SumT\) 是递增的,也就是说斜率是递增的。
那么我们每次可以把所有在队头的斜率比当前斜率小的点给弹出去,找 \(f_j\) 时直接找队头。这样可以大大减少时间。
时间复杂度是 \(O(n)\)。
一定不要 像我一样 在移项的时候推错式子!!!
代码
点击查看代码
namespace DP{
inline ll x(ll i){return sc[i];}
inline ll y(ll i){return f[i];}
inline ll k(ll i){return st[i]+s;}
inline ll b(ll i){return f[i]-st[i]*sc[i]-s*sc[n];}
void Dp(){
ll q[N]={0},hd=1,tl=1;
memset(q,0,sizeof(q));
_for(i,1,n){
#define h(o) q[hd+o]
#define t(o) q[tl-o]
while(hd<tl&&(y(h(1))-y(h(0)))<=k(i)*(x(h(1))-x(h(0))))
++hd;
ll j=h(0);
f[i]=y(j)-k(i)*x(j)-b(i);
f[i]=f[j]+st[i]*(sc[i]-sc[j])+s*(sc[n]-sc[j]);
while(hd<tl&&(x(t(0))-x(t(1)))*(y(i)-y(t(0)))<=(x(i)-x(t(0)))*(y(t(0))-y(t(1))))
--tl;
q[++tl]=i;
#undef h
#undef t
}
return;
}
}
[SDOI2012]任务安排
题意
题意和上一个任务安排一样。
\(1 \le n \le 3 \times 10^5\),\(1 \le s \le 2^8\),$ \left| T_i \right| \le 2^8$,\(0 \le C_i \le 2^8\)。
思路
和上一个任务安排相比,这里的 \(T_i\) 可以为负数。
也就是说,此时我们的斜率 \(SumT_i+S\) 不再具有单调性,那么我们就不能把队头的元素弹出去了,而是用二分找最优点。
时间复杂度是 \(O(nlogn)\)。
代码
点击查看代码
namespace DP{
ll q[N]={0},hd=1,tl=1;
inline ll x(ll i){return sc[i];}
inline ll y(ll i){return f[i];}
inline ll k(ll i){return st[i]+s;}
inline ll b(ll i){return f[i]-st[i]*sc[i]-s*sc[n];}
inline ll fd(ll i){
ll l=hd,r=tl;
while(l<r){
ll mid=(l+r)>>1;
if(y(q[mid+1])-y(q[mid])<=k(i)*(x(q[mid+1])-x(q[mid])))
l=mid+1;
else r=mid;
}
return l;
}
void Dp(){
memset(q,0,sizeof(q));
_for(i,1,n){
#define h(o) q[hd+o]
#define t(o) q[tl-o]
ll j=q[fd(i)];
f[i]=y(j)-k(i)*x(j)-b(i);
while(hd<tl&&(x(t(0))-x(t(1)))*(y(i)-y(t(0)))<=(x(i)-x(t(0)))*(y(t(0))-y(t(1))))
--tl;
q[++tl]=i;
#undef h
#undef t
}
return;
}
}
任务安排 再改
题意
题意和上一个任务安排一样。
\(1 \le n \le 3 \times 10^5\),\(1 \le s \le 2^8\),$ \left| T_i \right| , \left| C_i \right| \le 2^8$。
思路
要用到平衡树或 CDQ 分治维护凸包。
但是作者还没学,所以它咕咕咕了。
练习题
[HNOI2008]玩具装箱
思路
随便推一推:
\]
\]
\]
\]
\]
此时显然:
x=j+Sum_j\\
y=f_j+(j+Sum_j)^2\\
k=2(i+Sum_i-1-L)\\
b=f_i-(i+Sum_i-1-L)^2\\
\end{cases}
\]
然后就可以优化了。
代码
点击查看代码
namespace DP{
ll q[N]={0},hd=1,tl=1;
inline ll x(ll i){return i+sum[i];}
inline ll y(ll i){return f[i]+(i+sum[i])*(i+sum[i]);}
inline ll k(ll i){return 2*(i+sum[i]-1-L);}
inline ll b(ll i){return f[i]-(i+sum[i]-1-L)*(i+sum[i]-1-L);}
void Dp(){
memset(q,0,sizeof(q));
_for(i,1,n){
#define h(o) q[hd+o]
#define t(o) q[tl-o]
while(hd<tl&&(y(h(1))-y(h(0)))<=k(i)*(x(h(1))-x(h(0))))
++hd;
ll j=h(0);
f[i]=y(j)-k(i)*x(j)-b(i);
while(hd<tl&&(y(t(0))-y(t(1)))*(x(i)-x(t(0)))>(y(i)-y(t(0)))*(x(t(0))-x(t(1))))
--tl;
q[++tl]=i;
#undef h
#undef t
}
return;
}
}
[APIO2010]特别行动队
思路
随便推一推:
\]
\]
\]
\]
此时显然:
x=Sum_j\\
y=f_j+a(Sum_j)^2-b\times Sum_j\\
k=2aSum_i\\
b=f_i-a(Sum_i)^2-b\times Sum_i-c\\
\end{cases}
\]
然后就可以优化了。
注意:此时求的是最大值,也就是说维护的是一个上凸包。此时只要把下凸包往上翻一下,改一改大于号小于号就好了。
差不多长这样:
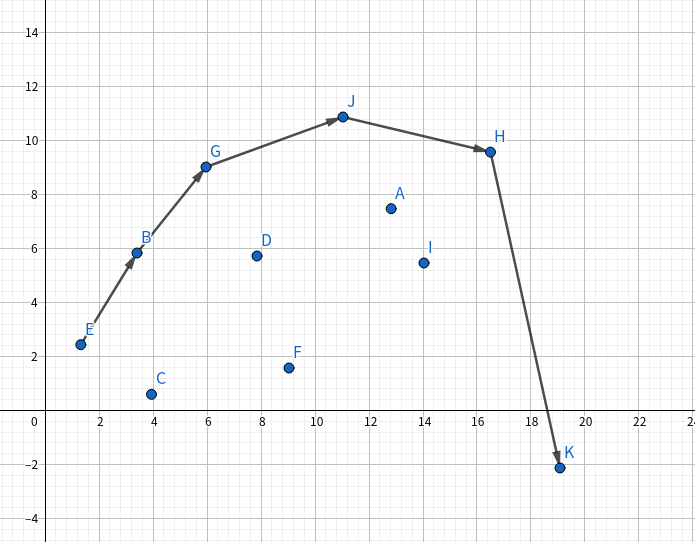
代码
点击查看代码
namespace DP{
ll q[N]={0},hd=1,tl=1;
inline ll X(ll i){return sum[i];}
inline ll Y(ll i){return f[i]+a*sum[i]*sum[i]-b*sum[i];}
inline ll K(ll i){return 2*a*sum[i];}
inline ll B(ll i){return f[i]-a*sum[i]*sum[i]-b*sum[i]-c;}
void Dp(){
memset(q,0,sizeof(q));
f[0]=0;
_for(i,1,n){
#define h(o) q[hd+o]
#define t(o) q[tl-o]
while(hd<tl&&(Y(h(1))-Y(h(0)))>=K(i)*(X(h(1))-X(h(0))))
++hd;
ll j=h(0);
f[i]=Y(j)-K(i)*X(j)-B(i);
while(hd<tl&&(Y(t(0))-Y(t(1)))*(X(i)-X(t(0)))<(Y(i)-Y(t(0)))*(X(t(0))-X(t(1))))
--tl;
q[++tl]=i;
#undef h
#undef t
}
return;
}
}
[ZJOI2007]仓库建设
思路
随便推一推:
\]
\]
\]
\]
此时显然:
x=SumP_j\\
y=f_j+SumPX_j\\
k=x_{i}\\
b=f_i-x_{i}*SumP_i+SumPX_i-c_{i}\\
\end{cases}
\]
然后就可以优化了。
但是这道题还有一个坑点:\(0\leq x_i,p_i,c_i<2^{31}\)。
也就是说有的山没有货物,有时我们可能不必在山脚建仓库,而是在一个之后的工厂都没有货物的工厂建仓库!
解决办法是加上下面的代码:
for_(i,n,1){
ans=min(ans,f[i]);
if(p[i])break;
}
代码
点击查看代码
namespace DP{
ll q[N]={0},hd=1,tl=1;
inline ll X(ll i){return sp[i];}
inline ll Y(ll i){return f[i]+spx[i];}
inline ll K(ll i){return x[i];}
inline ll B(ll i){return f[i]-x[i]*sp[i]+spx[i]-c[i];}
void Dp(){
memset(q,0,sizeof(q));
_for(i,1,n){
#define h(o) q[hd+o]
#define t(o) q[tl-o]
while(hd<tl&&(Y(h(1))-Y(h(0)))<=K(i)*(X(h(1))-X(h(0))))
++hd;
ll j=h(0);
f[i]=Y(j)-K(i)*X(j)-B(i);
while(hd<tl&&(Y(t(0))-Y(t(1)))*(X(i)-X(t(0)))>=(Y(i)-Y(t(0)))*(X(t(0))-X(t(1))))
--tl;
q[++tl]=i;
#undef h
#undef t
}
return;
}
}
[USACO08MAR]Land Acquisition G
思路
尝试直接推,但是发现推不出来。
首先可以发现一个性质:如果长方形 \(j\) 的长和宽都比长方形 \(i\) 的长和宽小,那么 \(j\) 可以直接并在 \(i\) 里面。
那么我们把这些土地以长为第一关键字,宽为第二关键字排序,把不会被完全覆盖的土地留下来,得到一些长单调递增,宽单调递减的土地。
如何实现这个操作?
排序之后长肯定是递增的。
如果一个宽比后面的小,那么它的长必然比后面的小,一定会被覆盖。
所以只要找出一个宽单调递减的序列就好了。
那么我们倒序遍历数组,记录当前的最大宽,如果当前宽比之前的最大宽大就加进去即可。
见代码GetLand部分。
然后就可以根据“长单调递增,宽单调递减”这个性质列出转移方程:
\]
\]
此时显然:
x=-h_j\\
y=f_j\\
k=w_i\\
b=f_i\\
\end{cases}
\]
然后就可以优化了。
代码
点击查看代码
namespace LAND{
inline bool cmp(Land a,Land b){
if(a.w==b.w)return a.h<b.h;
return a.w<b.w;
}
ll GetLand(){
sort(ld+1,ld+n+1,cmp);
ll len=0,max_h=0;
for_(i,n,1){
if(ld[i].h>max_h){
max_h=ld[i].h;
la[++len]=ld[i];
}
}
_for(i,1,len/2)swap(la[i],la[len-i+1]);
return len;
}
}
namespace DP{
ll q[N]={0},hd=1,tl=1;
inline ll X(ll i){return -la[i+1].h;}
inline ll Y(ll i){return f[i];}
inline ll K(ll i){return la[i].w;}
void Dp(){
memset(q,0,sizeof(q));
_for(i,1,n){
#define h(o) q[hd+o]
#define t(o) q[tl-o]
while(hd<tl&&(Y(h(1))-Y(h(0)))<=K(i)*(X(h(1))-X(h(0))))
++hd;
ll j=h(0);
f[i]=Y(j)-K(i)*X(j);
while(hd<tl&&(Y(t(0))-Y(t(1)))*(X(i)-X(t(0)))>(Y(i)-Y(t(0)))*(X(t(0))-X(t(1))))
--tl;
q[++tl]=i;
#undef h
#undef t
}
return;
}
}
\]
「学习笔记」斜率优化dp的更多相关文章
- 「学习笔记」wqs二分/dp凸优化
[学习笔记]wqs二分/DP凸优化 从一个经典问题谈起: 有一个长度为 \(n\) 的序列 \(a\),要求找出恰好 \(k\) 个不相交的连续子序列,使得这 \(k\) 个序列的和最大 \(1 \l ...
- 学习笔记:斜率优化DP
作为数学渣,先复习一下已知两点\((x_1, y_1)\), \((x_2, y_2)\),怎么求过两点的一次函数的斜率... 待定系数法代入 \(y = kx + b\) 有: \(x_1k + b ...
- hdu3507 斜率优化学习笔记(斜率优化+dp)
QWQ菜的真实. 首先来看这个题. 很显然能得到一个朴素的\(dp\)柿子 \[dp[i]=max(dp[i],dp[j]+(sum[i]-sum[j])^2) \] 但是因为\(n\le 50000 ...
- 「学习笔记」FFT 之优化——NTT
目录 「学习笔记」FFT 之优化--NTT 前言 引入 快速数论变换--NTT 一些引申问题及解决方法 三模数 NTT 拆系数 FFT (MTT) 「学习笔记」FFT 之优化--NTT 前言 \(NT ...
- 「学习笔记」FFT 快速傅里叶变换
目录 「学习笔记」FFT 快速傅里叶变换 啥是 FFT 呀?它可以干什么? 必备芝士 点值表示 复数 傅立叶正变换 傅里叶逆变换 FFT 的代码实现 还会有的 NTT 和三模数 NTT... 「学习笔 ...
- 「学习笔记」字符串基础:Hash,KMP与Trie
「学习笔记」字符串基础:Hash,KMP与Trie 点击查看目录 目录 「学习笔记」字符串基础:Hash,KMP与Trie Hash 算法 代码 KMP 算法 前置知识:\(\text{Border} ...
- 「学习笔记」Min25筛
「学习笔记」Min25筛 前言 周指导今天模拟赛五分钟秒第一题,十分钟说第二题是 \(\text{Min25}\) 筛板子题,要不是第三题出题人数据范围给错了,周指导十五分钟就 \(\text{AK ...
- 「学习笔记」Treap
「学习笔记」Treap 前言 什么是 Treap ? 二叉搜索树 (Binary Search Tree/Binary Sort Tree/BST) 基础定义 查找元素 插入元素 删除元素 查找后继 ...
- 「学习笔记」单调队列优化dp
目录 算法 例题 最大子段和 题意 思路 代码 修剪草坪 题意 思路 代码 瑰丽华尔兹 题意 思路 代码 股票交易 题意 思路 代码 算法 使用单调队列优化dp 废话 对与一些dp的转移方程,我们可以 ...
随机推荐
- 聊聊 C++ 和 C# 中的 lambda 玩法
这几天在看 C++ 的 lambda 表达式,挺有意思,这个标准是在 C11标准 加进去的,也就是 2011 年,相比 C# 2007 还晚了个 4 年, Lambda 这东西非常好用,会上瘾,今天我 ...
- 线程崩溃为什么不会导致 JVM 崩溃
大家好,我是坤哥 网上看到一个很有意思的据说是美团的面试题:为什么线程崩溃崩溃不会导致 JVM 崩溃,这个问题我看了不少回答,但都没答到根本原因,所以决定答一答,相信大家看完肯定会有收获,本文分以下几 ...
- 【Java面试】请简单说一下你对受检异常和非受检异常的理解
Hi,我是Mic 今天给大家分享一道阿里一面的面试题. 这道题目比较基础,但是确难倒了很多人. 关于"受检异常和非受检异常的理解" 我们来看看普通人和高手的回答. 普通人: 嗯.. ...
- WPF开发随笔收录-DrawingVisual绘制高性能曲线图
一.前言 项目中涉及到了心率监测,而且数据量达到了百万级别,通过WPF实现大数据曲线图时,尝试过最基础的Canvas来实现,但是性能堪忧,而且全部画出来也不实际.同时也尝试过找第三方的开源库,但是因为 ...
- Linux文本管理命令
touch命令: 创建空文件:touch newfile 也可以使用重定向符(>)创建空文件: > newfile 刷新文件时间: touch 已经存在的文件 cp命令:文件的复制 选项: ...
- Python快速下载商品数据,并连接数据库,保存数据
开发环境 python 3.8 pycharm 2021.2 专业版 代码实现 发送请求 获取数据 解析数据(筛选数据) 保存数据 连接数据库 开始代码 请求数据 # 伪装 headers = { ' ...
- 一种让运行在CentOS下的.NET CORE的Web项目简单方便易部署的自动更新方案
一.项目运行环境 项目采用的是.NET5开发的Web系统,独立部署在省内异地多台CentOS服务器上,它们运行在甲方专网环境中(不接触互联网),甲方进行业务运作时(一段时间内)会要求异地服务器开机上线 ...
- 0基础就可以上手的Spark脚本开发-for Java
前言 最近由于工作需要,要分析大几百G的Nginx日志数据.之前也有过类似的需求,但那个时候数据量不多.一次只有几百兆,或者几个G.因为数据都在Hive里面,当时的做法是:把数据从Hive导到MySQ ...
- jdbc 04: 配置连接信息
jdbc连接mysql,将需要的信息配置到文件中 package com.examples.jdbc.o4_配置连接信息; import java.sql.Connection; import jav ...
- 2509-Druid监控功能的深入使用与配置-基于SpringBoot-完全使用 .properties配置文件
java实现的数据库连接池有很多,c3p0,dbcp等,还有号称速度最快的HikariCP,并且springboot2.0.2版本默认使用的就是HikariCP. 为什么选用Druid呢? - 性能够 ...
