LeetCode 84. 柱状图中最大的矩形（Largest Rectangle in Histogram）

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

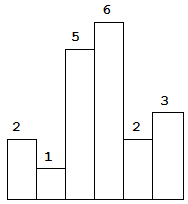
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

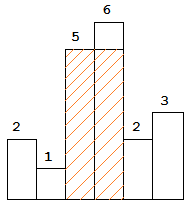
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

解题思路

这道题跟LeetCode 11很相似，但是因为考虑柱子宽度，因此解题技巧不相同，此题考查单调栈的应用。我们首先在数组最后加入0，这是为了方便处理完数组中的所有高度数据。假设存储高度坐标的栈为stack，当前处理的高度坐标为i(i∈[0→n])：

1. 如果当前stack为空，或者heights[i]大于等于栈顶坐标对应高度，则将i加入stack中，并将i加一；
2. 如果heights[i]小于栈顶坐标对应高度，说明可以开始处理栈内的坐标形成的局部递增高度，以求得当前最大矩形面积。弹出当前栈顶坐标 = top，此时栈顶新坐标 = top'，那么对应计算面积的宽度w = i - 1 - top'（若弹出栈顶坐标后，stack为空，则对应w = i），得到面积s = heights[top] * w，再次返回2检查栈；
3. 遍历完成i∈[0→n]，返回最大矩形面积。

代码

 class Solution {
 public:
     int largestRectangleArea(vector<int>& heights) {
         stack<int> s;
         int i = , maxArea = ;
         heights.push_back();
         while(i < heights.size()){
             if(s.empty() || heights[s.top()] <= heights[i]){
                 s.push(i);
                 i++;
             }
             else{
                 int top = s.top();
                 s.pop();
                 int l = s.empty() ? i : i - s.top() - ;
                 maxArea = max(maxArea, heights[top] * l);
             }
         }
         return maxArea;
     }
 };

参考自

LeetCode 84. Largest Rectangle in Histogram（直方图中最大矩形面积）