基于递归的BFS（Level-order）

上篇中学习了二叉树的DFS深度优先搜索算法，这次学习另外一种二叉树的搜索算法：BFS,下面看一下它的概念：

有些抽象是不？下面看下整个的遍历过程的动画演示就晓得是咋回事啦：

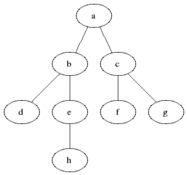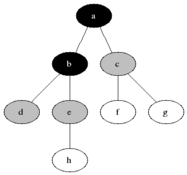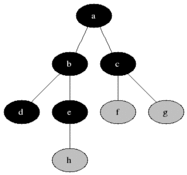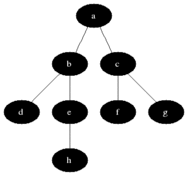
了解其概念之后，下面看下如何实现它？在正式实现逐层遍历之前，需要解决一个问题，那就是：得知道该树有多少层，也就是树的深度如何计算，下面来解决这个问题：

还是基于上篇的搜索二叉树的代码进行实现：

public class BinarySearchTree {
    TreeNode root = null;
 
    class TreeNode{
      int value;
      int position;
      TreeNode left = null, right = null;
      TreeNode(int value, int position){
        this.value = value;
        this.position = position;
      }
    }
 
    public void add(int value, int position){
      if(root == null){//生成一个根结点
        root = new TreeNode(value, position);
      } else {
        //生成叶子结点
        add(value, position, root);
      }
    }
 
    private void add(int value, int position, TreeNode node){
      if(node == null)
        throw new RuntimeException("treenode cannot be null");
      if(node.value == value)
        return; //ignore the duplicated value
      if(value < node.value){
        if(node.left == null){
          node.left = new TreeNode(value, position);
        }else{
          add(value, position, node.left);
        }
      }else{
        if(node.right == null){
          node.right = new TreeNode(value, position);
        }else{
          add(value, position, node.right);
        }
      }
    }
 
    //打印构建的二叉搜索树
    static void printTreeNode(TreeNode node) {
      if(node == null)
        return;
      System.out.println("node:" + node.value);
      if(node.left != null) {
        printTreeNode(node.left);
      }
      if(node.right != null) {
        printTreeNode(node.right);
      }
    }
 
    //搜索结点
    public int search(int value){
      return search(value, root);
    }
 
    private int search(int value, TreeNode node){
      if(node == null)
        return -1; //not found
      else if(value < node.value){
        System.out.println("Searching left");
        return search(value, node.left);
      }
      else if(value > node.value){
        System.out.println("Searching right");
        return search(value, node.right);
      }
      else
        return node.position;
    }
 
    //二叉树DFS遍历
    public void travel(){
      travel(root);
    }
    public void travel(TreeNode node){
      if(node == null)
        return;
      travel(node.left);
      travel(node.right);
      System.out.println(" " + node.value);
    }
 
    //二叉树的深度数
    public int depth(){
      return depth(root);
    }
 
    private int depth(TreeNode node){
      if(node == null)
        return 0;
      int leftDepth = depth(node.left);
      int rightDepth = depth(node.right);
      return Math.max(leftDepth, rightDepth) + 1;
    }
 
    public static void main(String[] args) {
      BinarySearchTree bst = new BinarySearchTree();
      int a[] = { 5, 8, 3, 4, 1, 7, 6};
      for(int i = 0; i < a.length; i++){
        bst.add(a[i], i);
      }
 
      System.out.println("Tree Depth:" + bst.depth());
    }
 
}

其上面搜索二叉树再贴一下，以便可以直观的可以查看：

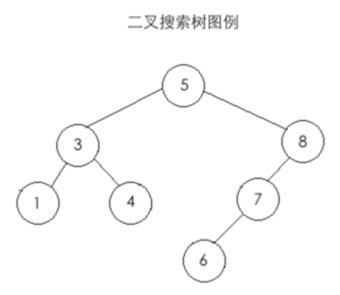
编译运行：

下面来debug看一下程序看如何计算出树的深度的：

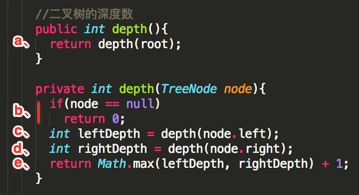
a、将root = TreeNode(5, 0)传给带参数的depth方法进行递归遍历。

Loop1：其参数node = TreeNode(5, 0)

　　b、,条件不满足，执行步骤c;

　　c、,int leftDepth = depth(node.left = TreeNode(3, 2)),继续递归左结点：

　　　　cb、,条件不满足，执行步骤cc;

　　　　cc、,int leftDepth = depth(node.left = TreeNode(1, 4)),继续递归左结点：

　　　　　　ccb、,条件不满足，执行步骤ccc;

　　　　　　ccc、,int leftDepth = depth(node.left = null),继续递归左结点：

　　　　　　　　cccb、,条件满足退出返回leftDepth = 0，执行步骤ccd;
　　　　　　ccd、,int rightDepth = depth(node.right = null),继续递归右结点:

　　　　　　　　cccb、,条件满足退出返回rightDepth = 0，执行步骤cce;

　　　　　　cce、,result = 1;　

　　　　所以这时leftDepth = 1;　　

　　　　cd、,int rightDepth = depth(node.right = TreeNode(4, 3)),继续递归右结点:

　　　　　　cdb、,条件不满足，执行步骤cdc;

　　　　　　cdc、,int leftDepth = depth(node.left = null),继续递归左结点：

　　　　　　　　cdcb、,条件满足退出返回leftDepth = 0，执行步骤cdd;
　　　　　　cdd、,int rightDepth = depth(node.right = null),继续递归右结点:

　　　　　　　　cddb、,条件满足退出返回rightDepth = 0，执行步骤cde;

　　　　　　cde、,result = 1;　
　　　　所以这时leftDepth = 1;

　　　　ce、,result = max(1, 1) + 1 = 2;

　　所以这时leftDepth = 2;

　　d、,int rightDepth = depth(node.right = TreeNode(8, 1)),继续递归右结点：

　　　　db、,条件不满足，执行步骤dc;

　　　　dc、,int leftDepth = depth(node.left = TreeNode(7, 5)),继续递归左结点：

　　　　　　dcb、,条件不满足，执行步骤dcc;

　　　　　　dcc、,int leftDepth = depth(node.left = TreeNode(6, 6)),继续递归左结点：

　　　　　　　　dccb、,条件不满足，执行步骤dccc;

　　　　　　　　dccc、,int leftDepth = depth(node.left = null),继续递归左结点：
　　　　　　　　　　dcccb、,条件满足退出返回leftDepth = 0，执行步骤dccd;

　　　　　　　　dccd、,int rightDepth = depth(node.right = null),继续递归右结点:

　　　　　　　　　　dccdb、,条件满足退出返回rightDepth = 0，执行步骤dcce;　

　　　　　　　　dcce、,result = max(0, 0) + 1 = 1;

　　　　　　所以这时leftDepth = 1;　　

　　　　　　dcd、,int rightDepth = depth(node.right = null),继续递归右结点:

　　　　　　　　dcdb、,条件满足退出返回rightDepth = 0，执行步骤dce;

　　　　　　dce、,result = max(1, 0) + 1 = 2;　

　　　　所以这时leftDepth = 2;

　　　　dd、,int rightDepth = depth(node.right = null),继续递归右结点:

　　　　　　ddb、,条件满足退出返回rightDepth = 0，执行步骤de;

　　　　所以这时rightDepth = 0;

　　　　de、,result = max(2, 0) + 1 = 3;

　　所以这时rightDepth = 3;

　　e、,result = max(2,3) + 1 = 4,所以最终此树的深度为4！

总结其实现思路：

1、递归的边界结束条件是传过来的节点为空了。

2、递归左结点的深度

3、递归右结点的深度

4、总结点的深度为左结点的深度+右结点的深度+1

上面已经实现了树的深度的计算，接下来则是利用DFS来将二叉树进行遍历啦，先上代码：

public class BinarySearchTree {
    TreeNode root = null;
 
    class TreeNode{
      int value;
      int position;
      TreeNode left = null, right = null;
      TreeNode(int value, int position){
        this.value = value;
        this.position = position;
      }
    }
 
    public void add(int value, int position){
      if(root == null){//生成一个根结点
        root = new TreeNode(value, position);
      } else {
        //生成叶子结点
        add(value, position, root);
      }
    }
 
    private void add(int value, int position, TreeNode node){
      if(node == null)
        throw new RuntimeException("treenode cannot be null");
      if(node.value == value)
        return; //ignore the duplicated value
      if(value < node.value){
        if(node.left == null){
          node.left = new TreeNode(value, position);
        }else{
          add(value, position, node.left);
        }
      }else{
        if(node.right == null){
          node.right = new TreeNode(value, position);
        }else{
          add(value, position, node.right);
        }
      }
    }
 
    //打印构建的二叉搜索树
    static void printTreeNode(TreeNode node) {
      if(node == null)
        return;
      System.out.println("node:" + node.value);
      if(node.left != null) {
        printTreeNode(node.left);
      }
      if(node.right != null) {
        printTreeNode(node.right);
      }
    }
 
    //搜索结点
    public int search(int value){
      return search(value, root);
    }
 
    private int search(int value, TreeNode node){
      if(node == null)
        return -1; //not found
      else if(value < node.value){
        System.out.println("Searching left");
        return search(value, node.left);
      }
      else if(value > node.value){
        System.out.println("Searching right");
        return search(value, node.right);
      }
      else
        return node.position;
    }
 
    //二叉树DFS遍历
    public void travel(){
      travel(root);
    }
    public void travel(TreeNode node){
      if(node == null)
        return;
      travel(node.left);
      travel(node.right);
      System.out.println(" " + node.value);
    }
 
    //二叉树的深度数
    public int depth(){
      return depth(root);
    }
 
    private int depth(TreeNode node){
      if(node == null)
        return 0;
      int leftDepth = depth(node.left);
      int rightDepth = depth(node.right);
      return Math.max(leftDepth, rightDepth) + 1;
    }
 
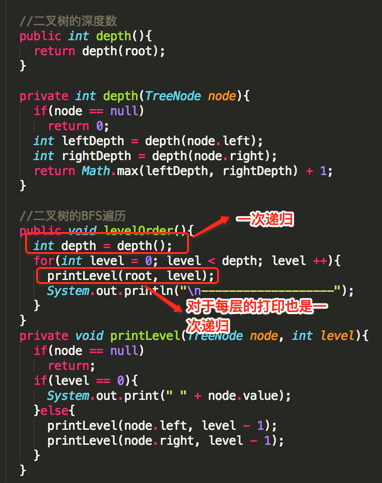
    //二叉树的BFS遍历
    public void levelOrder(){
      int depth = depth();
      for(int level = 0; level < depth; level ++){
        printLevel(root, level);
        System.out.println("\n-------------------");
      }
    }
    private void printLevel(TreeNode node, int level){
      if(node == null)
        return;
      if(level == 0){
        System.out.print(" " + node.value);
      }else{
        printLevel(node.left, level - 1);
        printLevel(node.right, level - 1);
      }
    }
 
    public static void main(String[] args) {
      BinarySearchTree bst = new BinarySearchTree();
      int a[] = { 5, 8, 3, 4, 1, 7, 6};
      for(int i = 0; i < a.length; i++){
        bst.add(a[i], i);
      }
 
      System.out.println("Tree Depth:" + bst.depth());
      bst.levelOrder();
    }
 
}

编译运行：

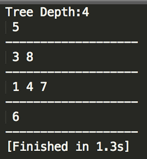
下面再来debug一下其利用递归来BFS遍历的整个过程：

a、depth = 4

b、根据树的层次依次进行遍历打印，具体如下：

　　Loop1：level = 0，level < 4条件为真，进入循环体：

　　　　①、递归打印第一层的所有结点：printLevel(root = TreeNode(5, 0), 0):

　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　d、条件为真，直接打印"5"【level=0表示当前就是要打印的结点，因为每递归一次层会递减一，等到指定层也就减为0了】

　　　　②、打印一个分隔行以便结果可以看起来比较直观。"-------------------"

　　　　level = level + 1 = 1;

　　Loop2：level = 1，level < 4条件为真，进入循环体：

　　　　①、递归打印第一层的所有结点：printLevel(root = TreeNode(5, 0), 1):

　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　d、条件为假，继续执行e;

　　　　　　e、分别递归左右结点：

　　　　　　　　①、printLevel(node.left = TreeNode(3, 2), 0);

　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　d、条件为真，直接打印"3";

　　　　　　　　②、printLevel(node.right = TreeNode(8, 1), 0);

　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　d、条件为真，直接打印"8";

　　　　②、打印一个分隔行以便结果可以看起来比较直观。"-------------------"

　　　　level = level + 1 = 2;

　　Loop3：level = 2，level < 4条件为真，进入循环体：

　　　　①、递归打印第一层的所有结点：printLevel(root = TreeNode(5, 0), 2):

　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　d、条件为假，继续执行e;

　　　　　　e、分别递归左右结点：

　　　　　　　　①、printLevel(node.left = TreeNode(3, 2), 1);

　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　d、条件为假，继续执行e;

　　　　　　　　　　e、分别递归左右结点：
　　　　　　　　　　　　①、printLevel(node.left = TreeNode(1, 4), 0);　　　

　　　　　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　　　　　d、条件为真，直接打印"1";

　　　　　　　　　　　　②、printLevel(node.right = TreeNode(4, 3), 0);

　　　　　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　　　　　d、条件为真，直接打印"4";

　　　　　　　　②、printLevel(node.right = TreeNode(8, 1), 1);

　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　d、条件为假，继续执行e;

　　　　　　　　　　e、分别递归左右结点：
　　　　　　　　　　　　①、printLevel(node.left = TreeNode(7, 5), 0);　　　

　　　　　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　　　　　d、条件为真，直接打印"7";

　　　　　　　　　　　　②、printLevel(node.right = null);

　　　　　　　　　　　　　　c、判断node是否为null，条件为真，直接返回递归结束。

　　　　②、打印一个分隔行以便结果可以看起来比较直观。"-------------------"

　　　　level = level + 1 = 3;

　　Loop4：level = 3，level < 4条件为真，进入循环体：

　　　　①、递归打印第一层的所有结点：printLevel(root = TreeNode(5, 0), 3):

　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　d、条件为假，继续执行e;

　　　　　　e、分别递归左右结点：

　　　　　　　　①、printLevel(node.left = TreeNode(3, 2), 2);

　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　d、条件为假，继续执行e;

　　　　　　　　　　e、分别递归左右结点：
　　　　　　　　　　　　①、printLevel(node.left = TreeNode(1, 4), 1);　　　

　　　　　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　　　　　d、条件为假，继续执行e;

　　　　　　　　　　　　　　e、分别递归左右结点：

　　　　　　　　　　　　　　　　①、printLevel(node.left = null, 0);

　　　　　　　　　　　　　　　　　　c、判断node是否为null，条件为真，直接返回递归结束。

　　　　　　　　　　　　　　　　②、printLevel(node.right = null, 0);　　　　

　　　　　　　　　　　　　　　　　　c、判断node是否为null，条件为真，直接返回递归结束。　　　　　　　　　　　　

　　　　　　　　　　　　②、printLevel(node.right = TreeNode(4, 3), 1);

　　　　　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　　　　　d、条件为假，继续执行e;

　　　　　　　　　　　　　　e、分别递归左右结点：

　　　　　　　　　　　　　　　　①、printLevel(node.left = null, 0);

　　　　　　　　　　　　　　　　　　c、判断node是否为null，条件为真，直接返回递归结束。

　　　　　　　　　　　　　　　　②、printLevel(node.right = null, 0);　　　　

　　　　　　　　　　　　　　　　　　c、判断node是否为null，条件为真，直接返回递归结束。　　

　　　　　　　　②、printLevel(node.right = TreeNode(8, 1), 2);

　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　d、条件为假，继续执行e;

　　　　　　　　　　e、分别递归左右结点：
　　　　　　　　　　　　①、printLevel(node.left = TreeNode(7, 5), 1);　　　

　　　　　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　　　　　d、条件为假，继续执行e;

　　　　　　　　　　　　　　e、分别递归左右结点：

　　　　　　　　　　　　　　　　①、printLevel(node.left = TreeNode(6, 6), 0);　　　

　　　　　　　　　　　　　　　　　　c、判断node是否为null，条件为假，继续执行d;

　　　　　　　　　　　　　　　　　　d、条件为真，直接打印"6";

　　　　　　　　　　　　　　　　②、printLevel(node.right = null);

　　　　　　　　　　　　　　　　　　c、判断node是否为null，条件为真，直接返回递归结束。

　　　　　　　　　　　　②、printLevel(node.right = null);

　　　　　　　　　　　　　　c、判断node是否为null，条件为真，直接返回递归结束。

　　　　②、打印一个分隔行以便结果可以看起来比较直观。"-------------------"

　　　　level = level + 1 = 4;

　　Loop5：level = 4，level < 4条件为假，结束循环。

总结其实现思路：

1、首先获得树的层数，然后进行逐层打印。

2、每层打印时，都是从根节点开始来遍历的【很显示这种做法不是很高效，这节先学一种，未来会有更高效的做法】

3、在递归函数中有三个条件：

　　a、如果当前节点是null，则直接返回递归结束。

　　b、如果当前的层数为0，那证明就是要打印的层，则直接打印当前节点。

　　c、以上两个条件都不满足，则说明该结点还有子结点，于是乎分别再次递归它的左结点和右结点，并且将层数减一。

下面来分析一下它的时间复杂度：

实际上整个算法是比较低效的，而上面的时间复杂度是O(n^2)级别的，未来会有更高效的O(n)线性级别的算法待学习，加油！