[BZOJ2208]:[Jsoi2010]连通数（暴力 or bitset or 塔尖？）

题目传送门

---

题目描述

度量一个有向图连通情况的一个指标是连通数，指图中可达顶点对的个数。

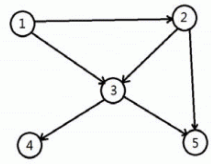
在上图中，顶点1可以到达1、2、3、4、5。

顶点2可以到达2、3、4、5。

顶点3可以到达3、4、5。

顶点4、5均只能到达自身，所以它的连通数为14。

请编写一个程序，输入一个图，求它的连通数。

---

输入格式

输入数据第一行是图顶点的数量，一个正整数N。 接下来N行，每行N个字符。第i行第j列的1表示顶点i到j有边，0则表示无边。

---

输出格式

输出一行一个整数，表示该图的连通数。

---

样例

样例输入：

3
010
001
100

样例输出：

9

---

数据范围与提示

对于100%的数据，N不超过2000。

---

题解

千万不要以为这道题数据范围N≤2000就可以暴力，N≤2000意味着最多会有$N^{2}$条边，dfs一遍遍历时间复杂度为边数，那么这道题就会被卡成$N^{3}$。

不过由于数据比较水，暴力卡常也可以A掉……

然而，占用评测资源显然是一种rp--的行为，所以考虑优化。

bitset！！！

利用floyed的思想。

空间和时间都在很大程度上得到了优化。

还不够快？

考虑塔尖缩点，一个强联通分量缩成一个点之后只要经过这个点，它里面的点都能被经过，所以记录size即可。

好吧，典型的空间换时间……

---

代码时刻

暴力：

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int nxt;
	int to;
}e[4000000];
int head[2001],cnt;
bool vis[2001];
long long ans;
char ch[2001];
void add(register int x,register int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
void dfs(register int x)
{
	vis[x]=1;
	ans++;
	for(register int i=head[x];i;i=e[i].nxt)
		if(!vis[e[i].to])dfs(e[i].to);
}
int main()
{
	int n;
	scanf("%d",&n);
	for(register int i=1;i<=n;i++)
	{
		scanf("%s",ch+1);
		for(register int j=1;j<=n;j++)if(ch[j]=='1')add(i,j);
	}
	for(register int i=1;i<=n;i++)memset(vis,0,sizeof(vis)),dfs(i);
	printf("%d",ans);
	return 0;
}
//推荐使用register进行卡常，评测机稍卡都有可能过不了，然而我5分钟1A了……

bitset优化：

#include<bits/stdc++.h>
using namespace std;
char ch[2001];
bitset<2001> a[2001];//bitset
int ans;
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",ch+1);
		for(int j=1;j<=n;j++)
			if(ch[j]=='1')a[i][j]=1;
		a[i][i]=1;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(a[j][i])a[j]|=a[i];//运用floyed思想
	for(int i=1;i<=n;i++)ans+=a[i].count();//统计答案
	cout<<ans<<endl;
	return 0;
}
//我觉得代码好小巧，你觉得呢？

塔尖+bitset：

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int nxt;
	int to;
}e[4000000],wzc[4000000];
int n;
int head[2001],cnt;
int headw[2001],cntw;
long long ans;
char ch[2001];
int dfn[2001],low[2001],sta[2001],ins[2001],c[2001],size[2001],num,top,tot;
int que[2001],d[2001],lft=1,rht=1;
bitset<2001> a[2001];
void add(int x,int y)//旧图
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
void add_w(int x,int y)//新图
{
	wzc[++cntw].nxt=headw[x];
	wzc[cntw].to=y;
	headw[x]=cntw;
}
void tarjan(int x)//缩点
{
	dfn[x]=low[x]=++num;
	sta[++top]=x;
	ins[x]=1;
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(!dfn[e[i].to])
		{
			tarjan(e[i].to);
			low[x]=min(low[x],low[e[i].to]);
		}
		else if(ins[e[i].to])
			low[x]=min(low[x],dfn[e[i].to]);
	}
	if(dfn[x]==low[x])
	{
		tot++;
		int y;
		do
		{
			y=sta[top--];
			ins[y]=0;
			c[y]=tot;
			size[tot]++;
		}while(x!=y);
	}
}
void build()//建新图
{
	for(int x=1;x<=n;x++)
		for(int i=head[x];i;i=e[i].nxt)
			if(c[x]!=c[e[i].to])
			{
				add_w(c[x],c[e[i].to]);
				d[c[e[i].to]]++;
			}
}
void _doudou()//统计答案
{
	for(int i=1;i<=tot;i++)
		if(!d[i])que[++rht]=i;
	while(lft<=rht)
	{
		a[que[lft]][que[lft]]=1;
		for(int i=headw[que[lft]];i;i=wzc[i].nxt)
		{
			a[wzc[i].to]|=a[que[lft]];
			d[wzc[i].to]--;
			if(!d[wzc[i].to])que[++rht]=wzc[i].to;
		}
		lft++;
	}
	for(int i=1;i<=tot;i++)
		for(int j=1;j<=tot;j++)
			if(a[i][j])ans+=size[i]*size[j];
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",ch+1);
		for(int j=1;j<=n;j++)if(ch[j]=='1')add(i,j);
	}
	for(int i=1;i<=n;i++)
		if(!dfn[i])tarjan(i);
	build();
	_doudou();
	printf("%d",ans);
	return 0;
}
//比较恶心，考试的时候建议使用前两种做法，这种做法仅供参考和装逼……

---

rp++