洛谷P1044栈（DP）

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即poppoppop（从栈顶弹出一个元素）和pushpushpush（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

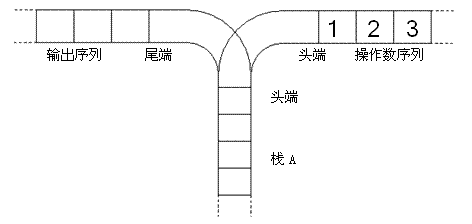
宁宁考虑的是这样一个问题：一个操作数序列，1,2,...,n1,2,...,n1,2,...,n（图示为1到3的情况），栈AAA的深度大于nnn。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的pushpushpush操作）

2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的poppoppop操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由1231 2 3123生成序列2312 3 1231的过程。

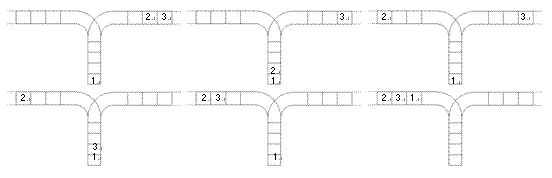
（原始状态如上图所示）

你的程序将对给定的nnn，计算并输出由操作数序列1,2,…,n1,2,…,n1,2,…,n经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数n(1≤n≤18)n(1≤n≤18)n(1≤n≤18)

输出格式

输出文件只有111行，即可能输出序列的总数目

输入输出样例

输入 #1

3

输出 #1

5
这题实际上是卡特兰数，既然标签是DP就考虑DP解法。设dp[i][j]表示i个数还没入栈，j个数在栈里，n-i-j个数已经出栈的最大方案数,则转移方程可以写出：dp[i][j]=dp[i-1][j+1]+dp[i][j-1]。要么选择把一个数入栈，要么选择一个数出栈。注意当j=0时即栈内没有数，这时候只能选择把一个数入栈。然后看边界，当i=0时，所有数要么在栈内要么已经出栈，这时候只有一种情况，所以赋值为1。要求的是dp[n][0]
所以i从1~n，j从0~n-i进行更新。可以看出，这个题是从结果（出栈序列已知的方案数）向初始情况更新。

#include <bits/stdc++.h>
using namespace std;
int dp[][]={};//dp[i][j]表示i个数还没入栈，j个数在栈里，n-i-j个数已经出栈的最大方案数 dp[i][j]=dp[i-1][j+1]+dp[i][j-1] //dp[0][j]=1 所有数都在栈里 只有一种方式
int main()
{
    int n;
    cin>>n;
    int i,j;
    dp[][]=;
    for(j=;j<=n;j++)dp[][j]=;
    for(i=;i<=n;i++)//注意是从1开始
    {
        for(j=;j<=n-i;j++)
        {
            if(j!=)dp[i][j]=dp[i-][j+]+dp[i][j-];
            else dp[i][j]=dp[i-][j+];
        }
     }
     cout<<dp[n][];
    return ;
}