Trie(字典树)的侃侃

Trie是什么 ？

字典树 ： 见名知意(在树上进行查询)。
         跟字典相关的必定与查询有密切的关系,
         查询就需要一定的媒介作为支撑,树就为这种查询提供支撑。

Trie做什么 ？

实现字符串快速检索的多叉树结构。
常见的字符串转化:小写字母或者大写字母组成的字符串,数字组成的字符串,01编码组成的字符串。

Trie有什么 ？

Trie 的每个节点都拥有若干个字符指针,就是说每个节点有多个子节点,通俗一点就是相当于古代
的大少爷可以有多个妻子。

Trie干什么 ？

1、插入(将一个字符串插入到字典树上)
2、检索(检索一个字符串 S 在Trie 上是否存在)

侃了这么多,看看这货到底是个啥 ？

假设有单词 : cab , cef , da 这样三个单词,那么这样三个单词组成的图是什么样的呢 ？
看下图 : (通常还要在末尾进行标记一下,表示到字符串的末尾)

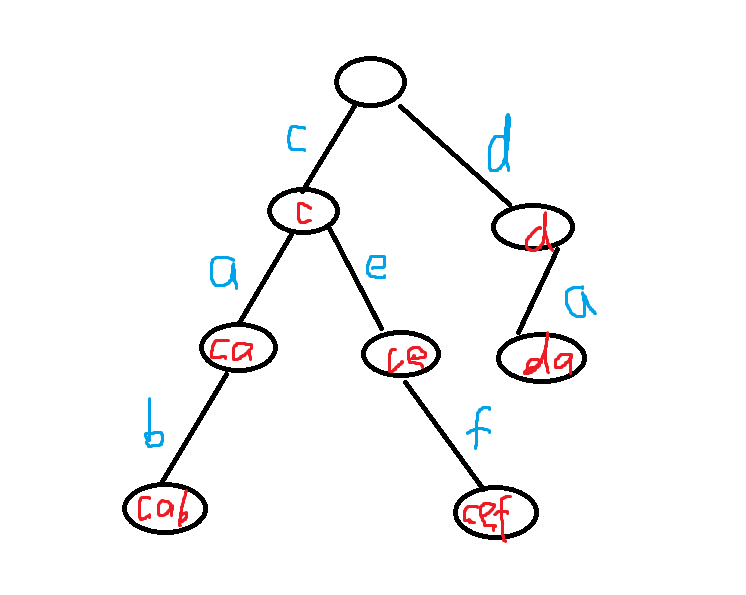
怎么实现这个玩意呢 ？

插入 :
像每个单词拼写一样,单词的开头就相当于是我们的根,从根节点出发,向儿子节点前进。
在向下走的过程中,看有没有当前这个字符的节点,如果有这个节点,就顺着这个节点继续
往下走,如果没有这个节点,就在这个节点之下再创建一个节点。
拿一个例子来说：
比如上图的 cab 和 cef, 先插入第一个字符串,从根节点出发,第一个字符是 c,我们发
现没有这个字符的节点,所以创建一个节点,将指针节点进行指向,然后一直向下移动,知道
字符串结尾。再插入第二个字符串,先检测第一个字符是否存在,我们发现存在,所以不用
创建,直接向下移动指针节点即可。
可以发现:
一个节点最多可以有26个孩子。
检索:
只需要将字符串遍历一遍，顺着根节点下来看这条路径上是否有不存在的值，即 0，如果
没有到末尾就发现有 0 ,说明这个字符串不存在,反之即存在。

Code :

插入:

void insert(char str[]) {
	int len = strlen(str),p = 0;                        // p 作为根节点从 0 开始
	for(int i = 0; i < len; i ++) {
		int ch = str[i] - 'a';
		if(trie[p][ch] == 0) trie[p][ch] = ++ idx;  // 创建新的节点
		p = trie[p][ch];                            // 指针移动
	}
	End[p] = true;                                      // 在末尾进行标记
	return ;
}

检索:

bool query(char str[]) {
	int len = strlen(str),p = 0;
	for(int i = 0; i < len; i ++ ){
		int ch = str[i] - '0';
		if(trie[p][ch] != 0) {
			p = trie[p][ch];
		} else {
			break;                            // 及时跳出
		}
	}
	return true;
}

Example: 前缀统计

        题目链接: https://www.acwing.com/problem/content/144/
        题目描述:给定N个字符串S1,S2…SN，接下来进行M次询问，每次询问给定一个字符串T，求S1～SN中有多少个字符串是T的前缀。
                输入字符串的总长度不超过106，仅包含小写字母。
                输入格式
                第一行输入两个整数N，M。
                接下来N行每行输入一个字符串Si。
                接下来M行每行一个字符串T用以询问。
                输出格式
                对于每个询问，输出一个整数表示答案。
                每个答案占一行。
                输入样例：
                    3 2
                    ab
                    bc
                    abc
                    abc
                    efg
                输出样例：
                    2
                    0

析题得说: 统计每个字符串出现的个数即可,用一个cnt[]数组记录每个字符串出现的个数,然后进行检索要处理的字符串,累加结果(模板题)

AC代码:

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int SIZE = 1e6 + 10;

int trie[SIZE][26],cnt[SIZE];
char str[SIZE];
int n,m,idx = 0;

int main(void) {
	void insert();
	int query();
	scanf("%d%d",&n,&m);
	for(int i = 1; i <= n; i ++) {
		scanf("%s",str);
		insert();
	}
	while(m --) {
		scanf("%s",str);
		printf("%d\n",query());
	}
	return 0;
} 

void insert() {
	int p = 0;
	for(int i = 0; i < strlen(str); i ++) {
		int ch = str[i] - 'a';
		if(trie[p][ch] == 0) trie[p][ch] = ++ idx;
		p = trie[p][ch];
	}
	cnt[p] ++;                            // 统计该字符串的个数
	return ;
}

int query() {
	int p = 0,res = 0;
	for(int i = 0 ; i < strlen(str); i ++) {
		int ch = str[i] - 'a';
		if(trie[p][ch] != 0) {
			p = trie[p][ch];
			res += cnt[p];           // 将以该字符结尾的数量累加,最后结果就是前缀字符串的数量
		} else {
		    break;
		}
	}
	return res;
}