19_05_01校内训练[polygon]

题意

把一个边长为1的正n边形放到一个正m边形中，要求m边形完全覆盖n边形，可以有交点，并且中心重合。求正m边形的最小边长，至少精确到6位。要求logn计算。

---

思考

先考虑m|n的情况。

我们知道，正m边形的边长与可行区域（即可以完全覆盖的那些角度）形成单射，当且仅当所有可行区域都成为可数的点时，答案最优。（可以理解为再缩小一点就无解了）

这样不难证明，把正n边形的几条边刚好卡在正m边形上是最优的。如n=8，m=4：

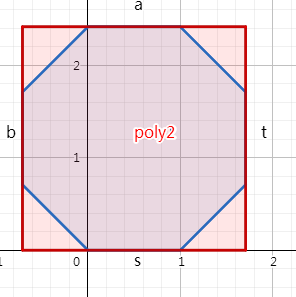
这时正m边形的边长是容易计算的。相信大家都会初中数学。

这样再考虑一般情况。由于是中心重合，正n边形旋转2π/m度后仍然是能被覆盖的。

在所有可行的旋转过程中，将最外圈的点连起来，仍然形成一个正多边形，且边数为lcm(n,m)。

例如，n=4，m=6：

用紫线围出来的正12边形即为正方形得到的结果。

至于正确性，在于所有的可行区域都是单点。

这样一来，就可以直接转化为上一个问题。公式认真推即可。

---

代码

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long int ll;
 const double pi=acos(-);
 ll n,m;
 ll gcd(ll x,ll y)
 {
     return x%y==?y:gcd(y,x%y);
 }
 ll lcm(ll x,ll y)
 {
     return x/gcd(x,y)*y;
 }
 double solve(ll n,ll m)
 {
     double len=/(*tan(pi/n));
     double th=(n/m)*pi/n;
     return tan(th)*len*;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     cin>>n>>m;
     double len=/(*sin(pi/n));
     n=lcm(n,m);
     double a=sin(pi/n)*len*;
     cout<<fixed<<setprecision()<<solve(n,m)*a<<endl;
     return ;
 }