leetcode-140-单词拆分②*

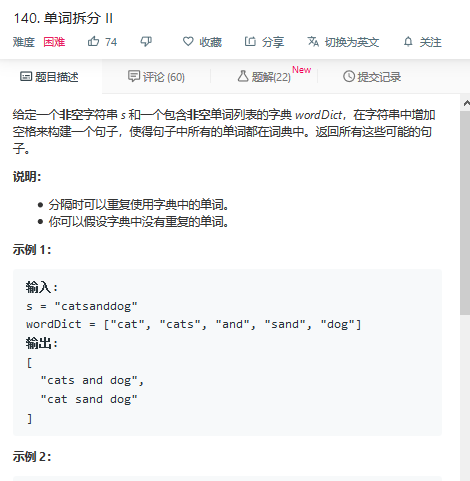
题目描述：

第一次提交：超时 O(N**N)

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        if not wordDict:return []
        res = []
        min_len,max_len = float("inf"),0
        for word in wordDict:
            min_len = min(len(word),min_len)
            max_len = max(len(word),max_len)
        res = []
        wordDict = set(wordDict)
        def helper(s,ans):
            if not s:
                res.append(ans[:-1])
                return
            for i in range(min_len,min(len(s)+1,max_len+1)):
                if s[:i] in wordDict:
                    helper(s[i:],ans+s[:i]+" ")

        helper(s,"")
        return res

方法一：记忆化回溯

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        import functools
        if not wordDict:return []
        wordDict = set(wordDict)
        max_len = max(map(len, wordDict))
        min_len = min(map(len,wordDict))
        @functools.lru_cache(None)
        def helper(s):
            res = []
            if not s:
                res.append("")
                return res
            for i in range(min_len-1,len(s)):
                if i < max_len and s[:i+1] in wordDict:
                    for t in helper(s[i+1:]):
                        if not t:
                            res.append(s[:i+1])
                        else:
                            res.append(s[:i+1] + " " + t)
            return res
        return helper(s)

另：加个判断，解一也能过

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        import functools
        if not self.wordBreak2(s,wordDict):return []
        if not wordDict:return []
        wordDict = set(wordDict)
        max_len = max(map(len, wordDict))
        min_len = min(map(len,wordDict))
        @functools.lru_cache(None)
        def helper(s):
            res = []
            if not s:
                res.append("")
                return res
            for i in range(min_len-1,len(s)):
                if i < max_len and s[:i+1] in wordDict:
                    for t in helper(s[i+1:]):
                        if not t:
                            res.append(s[:i+1])
                        else:
                            res.append(s[:i+1] + " " + t)
            return res
        return helper(s)

    def wordBreak2(self, s: str, wordDict: List[str]) -> bool:
        arr,wordSet=[0],set(wordDict)
        for i in range(len(s)):
            for j in arr[::-1]:
                if s[j:i+1] in wordSet:
                    arr.append(i+1)
                    break
        return arr[-1]==len(s)