ML: 降维算法-LDA

判别分析（discriminant analysis）是一种分类技术。它通过一个已知类别的“训练样本”来建立判别准则，并通过预测变量来为未知类别的数据进行分类。判别分析的方法大体上有三类，即Fisher判别、Bayes判别和距离判别。

• Fisher判别思想是投影降维，使多维问题简化为一维问题来处理。选择一个适当的投影轴,使所有的样品点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是：使每一组内的投影值所形成的组内离差尽可能小，而不同组间的投影值所形成的类间离差尽可能大。
• Bayes判别思想是根据先验概率求出后验概率，并依据后验概率分布作出统计推断。
• 距离判别思想是根据已知分类的数据计算各类别的重心，对未知分类的数据，计算它与各类重心的距离，与某个重心距离最近则归于该类

线性判别式分析（Linear Discriminant Analysis，简称为LDA）是模式识别的经典算法，在1996年由Belhumeur引入模式识别和人工智能领域。LDA的基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。

特征选择(亦即降维)是数据预处理中非常重要的一个步骤。对于分类来说，特征选择可以从众多的特征中选择对分类最重要的那些特征，去除原数据中的噪音。主成分分析(PCA)与线性判别式分析(LDA)是两种最常用的特征选择算法。但是他们的目标基本上是相反的，如下列示LDA与PCA之间的区别。

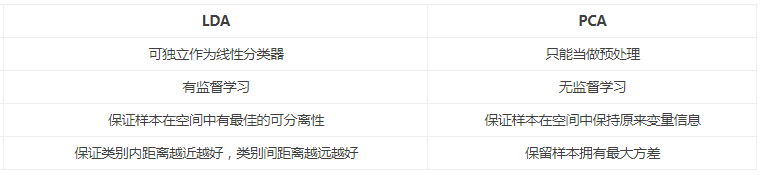
1. 出发思想不同。PCA主要是从特征的协方差角度，去找到比较好的投影方式，即选择样本点投影具有最大方差的方向；而LDA则更多的是考虑了分类标签信息，寻求投影后不同类别之间数据点距离更大化以及同一类别数据点距离最小化，即选择分类性能最好的方向。
2. 学习模式不同。PCA属于无监督式学习，因此大多场景下只作为数据处理过程的一部分，需要与其他算法结合使用，例如将PCA与聚类、判别分析、回归分析等组合使用；LDA是一种监督式学习方法，本身除了可以降维外，还可以进行预测应用，因此既可以组合其他模型一起使用，也可以独立使用。
3. 降维后可用维度数量不同。LDA降维后最多可生成C-1维子空间（分类标签数-1），因此LDA与原始维度数量无关，只有数据标签分类数量有关；而PCA最多有n维度可用，即最大可以选择全部可用维度。

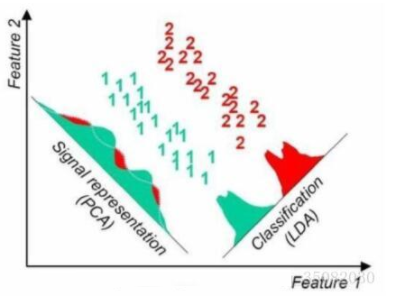
同一样例两种降维方法很直观的不同对比结果：

线性判别分析LDA算法由于其简单有效性在多个领域都得到了广泛地应用，是目前机器学习、数据挖掘领域经典且热门的一个算法；但是算法本身仍然存在一些局限性：

• 当样本数量远小于样本的特征维数，样本与样本之间的距离变大使得距离度量失效，使LDA算法中的类内、类间离散度矩阵奇异，不能得到最优的投影方向，在人脸识别领域中表现得尤为突出
• LDA不适合对非高斯分布的样本进行降维
• LDA在样本分类信息依赖方差而不是均值时，效果不好
• LDA可能过度拟合数据

LDA的应用应用场景：

• 人脸识别中的降维或模式识别
• 根据市场宏观经济特征进行经济预测
• 根据市场或用户不同属性进行市场调研
• 根据患者病例特征进行医学病情预测

MASS::lda

---

R中使用MASS包的lda函数实现线性判别。lda函数以Bayes判别思想为基础。当分类只有两种且总体服从多元正态分布条件下，Bayes判别与Fisher判别、距离判别是等价的。代码示例：

> if (require(MASS) == FALSE)
+ {
+   install.packages("MASS")
+ }
>
> model1=lda(Species~.,data=iris)
> table <- table(iris$Species,predict(model1)$class)
> table

             setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48         2
  virginica       0          1        49
> sum(diag(prop.table(table)))###判对率
[1] 0.98

结果可观察到判断错误的样本只有三个。在判别函数建立后，还可以类似主成分分析那样对判别得分进行绘图

> ld <- predict(model1)$x       #表示映射到模型中的向量上的值；即score值
> ds <- cbind(iris,as.data.frame(ld))
> head(ds)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species      LD1        LD2
1          5.1         3.5          1.4         0.2  setosa 8.061800  0.3004206
2          4.9         3.0          1.4         0.2  setosa 7.128688 -0.7866604
3          4.7         3.2          1.3         0.2  setosa 7.489828 -0.2653845
4          4.6         3.1          1.5         0.2  setosa 6.813201 -0.6706311
5          5.0         3.6          1.4         0.2  setosa 8.132309  0.5144625
6          5.4         3.9          1.7         0.4  setosa 7.701947  1.4617210
> p=ggplot(ds,mapping = aes(x=LD1,y=LD2))
> p+geom_point(aes(colour=Species),alpha=0.8,size=3)

再看一组基于主成份预测数据

> model2 <- lda(Species~LD1+LD2,ds)
> table(iris$Species,predict(model2)$class)

             setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48         2
  virginica       0          1        49

当不同类样本的协方差矩阵不同时，则应该使用二次判别。在使用lda和qda函数时注意：其假设是总体服从多元正态分布，若不满足的话则谨慎使用二次判别。

> iris.qda=qda(Species~.,data=iris,cv=T)
> table<-table(iris$Species,predict(iris.qda,iris)$class)
> table

             setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48         2
  virginica       0          1        49
> sum(diag(prop.table(table)))###判对率
[1] 0.98

CV参数设置为T，是使用留一交叉检验（leave-one-out cross-validation），并自动生成预测值。这种条件下生成的混淆矩阵较为可靠。此外还可以使用predict(model)$posterior提取后验概率