Codeforces Round #356 (Div. 2)

A. Bear and Five Cards

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A little bear Limak plays a game. He has five cards. There is one number written on each card. Each number is a positive integer.

Limak can discard (throw out) some cards. His goal is to minimize the sum of numbers written on remaining (not discarded) cards.

He is allowed to at most once discard two or three cards with the same number. Of course, he won't discard cards if it's impossible to choose two or three cards with the same number.

Given five numbers written on cards, cay you find the minimum sum of numbers on remaining cards?

Input

The only line of the input contains five integers t1, t2, t3, t4 and t5 (1 ≤ ti ≤ 100) — numbers written on cards.

Output

Print the minimum possible sum of numbers written on remaining cards.

Examples

input

7 3 7 3 20

output

26

input

7 9 3 1 8

output

28

input

10 10 10 10 10

output

20

Note

In the first sample, Limak has cards with numbers 7, 3, 7, 3 and 20. Limak can do one of the following.

• Do nothing and the sum would be 7 + 3 + 7 + 3 + 20 = 40.
• Remove two cards with a number 7. The remaining sum would be 3 + 3 + 20 = 26.
• Remove two cards with a number 3. The remaining sum would be 7 + 7 + 20 = 34.

You are asked to minimize the sum so the answer is 26.

In the second sample, it's impossible to find two or three cards with the same number. Hence, Limak does nothing and the sum is7 + 9 + 1 + 3 + 8 = 28.

In the third sample, all cards have the same number. It's optimal to discard any three cards. The sum of two remaining numbers is10 + 10 = 20.

记录判断

 #include <bits/stdc++.h>
 using namespace std;

 int main()
 {
     int i,j;
     int n;
     int a[],b[];
     memset(b,,sizeof(b));

     int sum=,ma=;
     for(i=;i<=;i++)
     {
         scanf("%d",&a[i]);
         b[a[i]]++;
         sum+=a[i];
     }

     for(i=;i<=;i++)
     {
         if(b[a[i]]>= && a[i]*>ma)
         {
             ma=a[i]*;
         }
         if(b[a[i]]>= && a[i]*>ma)
         {
             ma=a[i]*;
         }
     }

     printf("%d\n",sum-ma);
 }

 

B. Bear and Finding Criminals

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are n cities in Bearland, numbered 1 through n. Cities are arranged in one long row. The distance between cities i and j is equal to |i - j|.

Limak is a police officer. He lives in a city a. His job is to catch criminals. It's hard because he doesn't know in which cities criminals are. Though, he knows that there is at most one criminal in each city.

Limak is going to use a BCD (Bear Criminal Detector). The BCD will tell Limak how many criminals there are for every distance from a citya. After that, Limak can catch a criminal in each city for which he is sure that there must be a criminal.

You know in which cities criminals are. Count the number of criminals Limak will catch, after he uses the BCD.

Input

The first line of the input contains two integers n and a (1 ≤ a ≤ n ≤ 100) — the number of cities and the index of city where Limak lives.

The second line contains n integers t1, t2, ..., tn (0 ≤ ti ≤ 1). There are ti criminals in the i-th city.

Output

Print the number of criminals Limak will catch.

Examples

input

6 3
1 1 1 0 1 0

output

3

input

5 2
0 0 0 1 0

output

1

Note

In the first sample, there are six cities and Limak lives in the third one (blue arrow below). Criminals are in cities marked red.

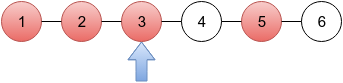
Using the BCD gives Limak the following information:

• There is one criminal at distance 0 from the third city — Limak is sure that this criminal is exactly in the third city.
• There is one criminal at distance 1 from the third city — Limak doesn't know if a criminal is in the second or fourth city.
• There are two criminals at distance 2 from the third city — Limak is sure that there is one criminal in the first city and one in the fifth city.
• There are zero criminals for every greater distance.

So, Limak will catch criminals in cities 1, 3 and 5, that is 3 criminals in total.

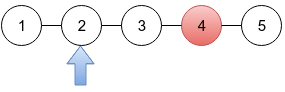
In the second sample (drawing below), the BCD gives Limak the information that there is one criminal at distance 2 from Limak's city. There is only one city at distance 2 so Limak is sure where a criminal is.

 #include <bits/stdc++.h>
 using namespace std;

 int main()
 {
     int n,a,ans;
     int i,j,b[];
     scanf("%d %d",&n,&a);
     for(i=;i<=n;i++)
     {
         scanf("%d",&b[i]);
     }
     ans=;
     for(i=;i<=n;i++)
     {
         if(a-i>=)
         {
             if(a+i<=n)
             {
                 if(b[a-i]== && b[a+i]==)
                     ans+=;
             }
             else
             {
                 if(b[a-i]==)
                     ans++;
             }
         }
         else
         {
             if(a+i<=n)
             {
                 if(b[a+i]==)
                     ans++;
             }
             else
                 break;
         }
     }
     if(b[a]==)
         ans++;
     printf("%d\n",ans);
     return ;
 }

C. Bear and Prime 100

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

This is an interactive problem. In the output section below you will see the information about flushing the output.

Bear Limak thinks of some hidden number — an integer from interval [2, 100]. Your task is to say if the hidden number is prime or composite.

Integer x > 1 is called prime if it has exactly two distinct divisors, 1 and x. If integer x > 1 is not prime, it's called composite.

You can ask up to 20 queries about divisors of the hidden number. In each query you should print an integer from interval [2, 100]. The system will answer "yes" if your integer is a divisor of the hidden number. Otherwise, the answer will be "no".

For example, if the hidden number is 14 then the system will answer "yes" only if you print 2, 7 or 14.

When you are done asking queries, print "prime" or "composite" and terminate your program.

You will get the Wrong Answer verdict if you ask more than 20 queries, or if you print an integer not from the range [2, 100]. Also, you will get the Wrong Answer verdict if the printed answer isn't correct.

You will get the Idleness Limit Exceeded verdict if you don't print anything (but you should) or if you forget about flushing the output (more info below).

Input

After each query you should read one string from the input. It will be "yes" if the printed integer is a divisor of the hidden number, and "no" otherwise.

Output

Up to 20 times you can ask a query — print an integer from interval [2, 100] in one line. You have to both print the end-of-line character and flush the output. After flushing you should read a response from the input.

In any moment you can print the answer "prime" or "composite" (without the quotes). After that, flush the output and terminate your program.

To flush you can use (just after printing an integer and end-of-line):

• fflush(stdout) in C++;
• System.out.flush() in Java;
• stdout.flush() in Python;
• flush(output) in Pascal;
• See the documentation for other languages.

Hacking. To hack someone, as the input you should print the hidden number — one integer from the interval [2, 100]. Of course, his/her solution won't be able to read the hidden number from the input.

Examples

input

yes
no
yes

output

2
80
5
composite

input

no
yes
no
no
no

output

58
59
78
78
2
prime

Note

The hidden number in the first query is 30. In a table below you can see a better form of the provided example of the communication process.

The hidden number is divisible by both 2 and 5. Thus, it must be composite. Note that it isn't necessary to know the exact value of the hidden number. In this test, the hidden number is 30.

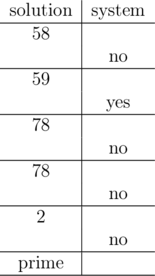
59 is a divisor of the hidden number. In the interval [2, 100] there is only one number with this divisor. The hidden number must be 59, which is prime. Note that the answer is known even after the second query and you could print it then and terminate. Though, it isn't forbidden to ask unnecessary queries (unless you exceed the limit of 20 queries).

交互题，系统给你一个2到100之间的数，依次与区间中的素数比较 由程序输入判断结果 最后判断是否素数

注意要特别判定 4 9 25 49的情况，因为这几个数只能是2 3 5 7的平方 循环中只记录了一次

 #include <bits/stdc++.h>
 using namespace std;

 int main()
 {
     int a[]={,,,,,,,,,,,,,,,,,,};
     int i,j,cnt=;
     char str[];
     for(i=;i<;i++)
     {
         printf("%d\n",a[i]);
         fflush(stdout);
         scanf("%s",str);
         if(str[]=='y')
             cnt++;
     }
     if(cnt>)
     {
         printf("composite\n");
         fflush(stdout);
     }
     else
     {
         printf("prime\n");
         fflush(stdout);
     }
     return ;
 }

D. Bear and Tower of Cubes

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Limak is a little polar bear. He plays by building towers from blocks. Every block is a cube with positive integer length of side. Limak has infinitely many blocks of each side length.

A block with side a has volume a3. A tower consisting of blocks with sides a1, a2, ..., ak has the total volume a13 + a23 + ... + ak3.

Limak is going to build a tower. First, he asks you to tell him a positive integer X — the required total volume of the tower. Then, Limak adds new blocks greedily, one by one. Each time he adds the biggest block such that the total volume doesn't exceed X.

Limak asks you to choose X not greater than m. Also, he wants to maximize the number of blocks in the tower at the end (however, he still behaves greedily). Secondarily, he wants to maximize X.

Can you help Limak? Find the maximum number of blocks his tower can have and the maximum X ≤ m that results this number of blocks.

Input

The only line of the input contains one integer m (1 ≤ m ≤ 1015), meaning that Limak wants you to choose X between 1 and m, inclusive.

Output

Print two integers — the maximum number of blocks in the tower and the maximum required total volume X, resulting in the maximum number of blocks.

Examples

input

48

output

9 42

input

6

output

6 6

Note

In the first sample test, there will be 9 blocks if you choose X = 23 or X = 42. Limak wants to maximize X secondarily so you should choose 42.

In more detail, after choosing X = 42 the process of building a tower is:

• Limak takes a block with side 3 because it's the biggest block with volume not greater than 42. The remaining volume is 42 - 27 = 15.
• The second added block has side 2, so the remaining volume is 15 - 8 = 7.
• Finally, Limak adds 7 blocks with side 1, one by one.

So, there are 9 blocks in the tower. The total volume is is 33 + 23 + 7·13 = 27 + 8 + 7 = 42.

题解：

Let's find the maximum a that a3 ≤ m. Then, it's optimal to choose X that the first block will have side a or a - 1. Let's see why.

• If the first block has side a then we are left with m2 = m - first_block = m - a3.
• If the first block has side a - 1 then the initial X must be at most a3 - 1 (because otherwise we would take a block with side a), so we are left with m2 = a3 - 1 - first_block = a3 - 1 - (a - 1)3
• If the first blocks has side a - 2 then the initial X must be at most (a - 1)3 - 1, so we are left withm2 = (a - 1)3 - 1 - first_block = (a - 1)3 - 1 - (a - 2)3.

We want to first maximize the number of blocks we can get with new limit m2. Secondarily, we want to have the biggest initial X. You can analyze the described above cases and see that the first block with side (a - 2)3 must be a worse choice than (a - 1)3. It's because we start with smaller X and we are left with smaller m2. The situation for even smaller side of the first block would be even worse.

Now, you can notice that the answer will be small. From m of magnitude a3 after one block we get m2 of magnitude a2. So, from m we go to m2 / 3, which means that the answer is O(loglog(m)). The exact maximum answer turns out to be 18.

The intended solution is to use the recursion and brutally check both cases: taking a3 and taking (a - 1)3 where a is maximum thata3 ≤ m. It's so fast that you can even find a in O(m1 / 3), increasing a by one.

 #include <bits/stdc++.h>
 using namespace std;

 pair <long long,long long>  ans;

 long long pow3(long long x)
 {
     return x*x*x;
 }

 void dfs(long long m,long long num,long long sum)
 {
     if(m==)
     {
         ans=max(ans,make_pair(num,sum));
         return;
     }

     long long x=;
     while(pow3(x+)<=m)   x++;

     dfs(m-pow3(x),num+,sum+pow3(x));
     if(x>)
         dfs(pow3(x)--pow3(x-),num+,sum+pow3(x-));
 }

 int main()
 {
     long long m;
     int i,j;
     ans.first=,ans.second=;
     scanf("%I64d",&m);
     dfs(m,,);
     printf("%I64d %I64d\n",ans.first,ans.second);
     return ;
 }

E. Bear and Square Grid

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You have a grid with n rows and n columns. Each cell is either empty (denoted by '.') or blocked (denoted by 'X').

Two empty cells are directly connected if they share a side. Two cells (r1, c1) (located in the row r1 and column c1) and (r2, c2) areconnected if there exists a sequence of empty cells that starts with (r1, c1), finishes with (r2, c2), and any two consecutive cells in this sequence are directly connected. A connected component is a set of empty cells such that any two cells in the component are connected, and there is no cell in this set that is connected to some cell not in this set.

Your friend Limak is a big grizzly bear. He is able to destroy any obstacles in some range. More precisely, you can choose a square of size k × k in the grid and Limak will transform all blocked cells there to empty ones. However, you can ask Limak to help only once.

The chosen square must be completely inside the grid. It's possible that Limak won't change anything because all cells are empty anyway.

You like big connected components. After Limak helps you, what is the maximum possible size of the biggest connected component in the grid?

Input

The first line of the input contains two integers n and k (1 ≤ k ≤ n ≤ 500) — the size of the grid and Limak's range, respectively.

Each of the next n lines contains a string with n characters, denoting the i-th row of the grid. Each character is '.' or 'X', denoting an empty cell or a blocked one, respectively.

Output

Print the maximum possible size (the number of cells) of the biggest connected component, after using Limak's help.

Examples

input

5 2
..XXX
XX.XX
X.XXX
X...X
XXXX.

output

10

input

5 3
.....
.XXX.
.XXX.
.XXX.
.....

output

25

Note

In the first sample, you can choose a square of size 2 × 2. It's optimal to choose a square in the red frame on the left drawing below. Then, you will get a connected component with 10 cells, marked blue in the right drawing.

思路：

Let's first find CC's (connected components) in the given grid, using DFS's.

We will consider every possible placement of a k × k square. When the placement is fixed then the answer is equal to the sum of k2 the the sum of sizes of CC's touching borders of the square (touching from outside), but for those CC's we should only count their cells that are outside of the square — not to count something twice. We will move a square, and at the same time for each CC we will keep the number of its cells outside the square.

We will used a sliding-window technique. Let's fix row of the grid — the upper row of the square. Then, we will first place the square on the left, and then we will slowly move a square to the right. As we move a square, we should iterate over cells that stop or start to belong to the square. For each such empty cell we should add or subtract 1 from the size of its CC (ids and sizes of CC's were found at the beginning).

And for each placement we consider, we should iterate over outside borders of the square (4k cells — left, up, right and down side) and sum up sizes of CC's touching our square. Be careful to not count some CC twice — you can e.g. keep an array of booleans and mark visited CC's. After checking all 4k cells you should clear an array, but you can't do it in O(number_of_all_components) because it would be too slow. You can e.g. also add visited CC's to some vector, and later in the boolean array clear only CC's from the vector (and then clear vector).

The complexity is O(n2·k).

 #include<bits/stdc++.h>
 using namespace std;
 const int nax = ;
 int n;
 char grid[nax][nax]; // input
 int cc[nax][nax]; // id of CC in which this cell is
 int cc_size[nax*nax]; // size of CC
 int when_added[nax*nax];

 const int dx[] = {-, , , };
 const int dy[] = {, , -, };
 const char EMPTY = '.';

 bool inside(int x, int y) {
     return  <= min(x, y) && max(x, y) < n;
 }

 void dfs(int x, int y, int which_cc) {
     cc[x][y] = which_cc;
     ++cc_size[which_cc];
     for(int i = ; i < ; ++i) { // iterate of 4 adjacent cells
         int x2 = x + dx[i];
         int y2 = y + dy[i];
         if(inside(x2, y2) && grid[x2][y2] == EMPTY && cc[x2][y2] == )
             dfs(x2, y2, which_cc);
     }
 }

 void add(int x, int y, int & answer, int current_time) {
     if(inside(x, y) && grid[x][y] == EMPTY) {
         int id = cc[x][y];
         if(when_added[id] != current_time) {
             when_added[id] = current_time;
             answer += cc_size[id];
         }
     }
 }

 int main()
 {
     int k;
     scanf("%d%d", &n, &k);
     for(int i = ; i < n; ++i)
         scanf("%s", grid[i]);

     // run DFS many times to find CC's (connected components)
     int how_many_cc = ;
     for(int x = ; x < n; ++x)
         for(int y = ; y < n; ++y)
             if(grid[x][y] == EMPTY && cc[x][y] == )
                 dfs(x, y, ++how_many_cc);

     int cur_time = ;
     int best_answer = ;

     for(int y_low = ; y_low + k <= n; ++y_low) {
         // first we put a square with corner in (0, y_low)
         for(int x = ; x < k; ++x)
             for(int y = y_low; y < y_low + k; ++y)
                 --cc_size[cc[x][y]]; // subtract cells inside a square

         for(int x_low = ; x_low  + k <= n; ++x_low) {
             int answer = k * k; // all cells inside a square
             // consider one row: below, above, left, right
             for(int x = x_low; x < x_low + k; ++x) {
                 add(x, y_low - , answer, cur_time);
                 add(x, y_low + k, answer, cur_time);
             }
             for(int y = y_low; y < y_low + k; ++y) {
                 add(x_low - , y, answer, cur_time);
                 add(x_low + k, y, answer, cur_time);
             }
             ++cur_time;
             best_answer = max(best_answer, answer);

             if(x_low + k != n) {
                 // move a square to increase x_low by 1
                 for(int y = y_low; y < y_low + k; ++y) {
                     ++cc_size[cc[x_low][y]]; // remove cells with x = x_low
                     --cc_size[cc[x_low+k][y]]; // insert cells with x = x_low+k
                 }
             }
         }

         for(int x = n - k; x < n; ++x)
             for(int y = y_low; y < y_low + k; ++y)
                 ++cc_size[cc[x][y]]; // we don't need cells inside to be subtracted
     }
     printf("%d\n", best_answer);

     return ;
 }