kmeans聚类理论篇

前言

kmeans是最简单的聚类算法之一，但是运用十分广泛。最近在工作中也经常遇到这个算法。kmeans一般在数据分析前期使用，选取适当的k，将数据分类后，然后分类研究不同聚类下数据的特点。

本文记录学习kmeans算法相关的内容，包括算法原理，收敛性，效果评估聚，最后带上R语言的例子，作为备忘。

 

算法原理

kmeans的计算方法如下：

1 随机选取k个中心点

2 遍历所有数据，将每个数据划分到最近的中心点中

3 计算每个聚类的平均值，并作为新的中心点

4 重复2-3，直到这k个中线点不再变化（收敛了），或执行了足够多的迭代

时间复杂度：O(I*n*k*m)

空间复杂度：O(n*m)

其中m为每个元素字段个数，n为数据量，I为跌打个数。一般I,k,m均可认为是常量，所以时间和空间复杂度可以简化为O(n)，即线性的。

 

算法收敛

从kmeans的算法可以发现，SSE其实是一个严格的坐标下降（Coordinate Decendet）过程。设目标函数SSE如下：

SSE(,,…,) =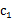

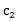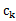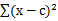
采用欧式距离作为变量之间的聚类函数。每次朝一个变量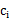的方向找到最优解，也就是求偏倒数，然后等于0，可得

c_i=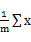 其中m是c_i所在的簇的元素的个数

也就是当前聚类的均值就是当前方向的最优解（最小值），这与kmeans的每一次迭代过程一样。所以，这样保证SSE每一次迭代时，都会减小，最终使SSE收敛。

由于SSE是一个非凸函数（non-convex function），所以SSE不能保证找到全局最优解，只能确保局部最优解。但是可以重复执行几次kmeans，选取SSE最小的一次作为最终的聚类结果。

 

0-1规格化

由于数据之间量纲的不相同，不方便比较。举个例子，比如游戏用户的在线时长和活跃天数，前者单位是秒，数值一般都是几千，而后者单位是天，数值一般在个位或十位，如果用这两个变量来表征用户的活跃情况，显然活跃天数的作用基本上可以忽略。所以，需要将数据统一放到0~1的范围，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。具体计算方法如下：

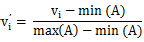
其中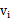属于A。

轮廓系数

轮廓系数（Silhouette Coefficient）结合了聚类的凝聚度（Cohesion）和分离度（Separation），用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果越好。具体计算方法如下：

1. 对于第i个元素x_i，计算x_i与其同一个簇内的所有其他元素距离的平均值，记作a_i，用于量化簇内的凝聚度。
2. 选取x_i外的一个簇b，计算x_i与b中所有点的平均距离，遍历所有其他簇，找到最近的这个平均距离,记作b_i，用于量化簇之间分离度。
3. 对于元素x_i，轮廓系数s_i = (b_i – a_i)/max(a_i,b_i)
4. 计算所有x的轮廓系数，求出平均值即为当前聚类的整体轮廓系数

从上面的公式，不难发现若s_i小于0，说明x_i与其簇内元素的平均距离小于最近的其他簇，表示聚类效果不好。如果a_i趋于0，或者b_i足够大，那么s_i趋近与1，说明聚类效果比较好。

 

K值选取

在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分类贴标签。所以k一般不会设置很大。可以通过枚举，令k从2到一个固定值如10，在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。

 

实际应用

下面通过例子（R实现，完整代码见附件）讲解kmeans使用方法，会将上面提到的内容全部串起来

library(fpc) # install.packages("fpc")
data(iris)
head(iris)

加载实验数据iris，这个数据在机器学习领域使用比较频繁，主要是通过画的几个部分的大小，对花的品种分类，实验中需要使用fpc库估计轮廓系数，如果没有可以通过install.packages安装。

# 0-1 正规化数据
min.max.norm <- function(x){
    (x-min(x))/(max(x)-min(x))
}
raw.data <- iris[,1:4]
norm.data <- data.frame(sl = min.max.norm(raw.data[,1]),
                                        sw = min.max.norm(raw.data[,2]),
                                        pl = min.max.norm(raw.data[,3]),
                                        pw = min.max.norm(raw.data[,4]))                            

对iris的4个feature做数据正规化，每个feature均是花的某个不为的尺寸。

# k取2到8，评估K
K <- 2:8
round <- 30 # 每次迭代30次，避免局部最优
rst <- sapply(K, function(i){
    print(paste("K=",i))
    mean(sapply(1:round,function(r){
        print(paste("Round",r))
        result <- kmeans(norm.data, i)
        stats <- cluster.stats(dist(norm.data), result$cluster)
        stats$avg.silwidth
    }))
})
plot(K,rst,type='l',main='轮廓系数与K的关系', ylab='轮廓系数')

评估k，由于一般K不会太大，太大了也不易于理解，所以遍历K为2到8。由于kmeans具有一定随机性，并不是每次都收敛到全局最小，所以针对每一个k值，重复执行30次，取并计算轮廓系数，最终取平均作为最终评价标准，可以看到如下的示意图，

 

 

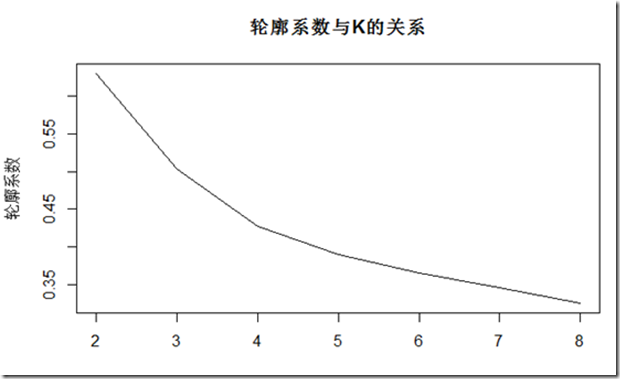
当k取2时，有最大的轮廓系数，虽然实际上有3个种类。

# 降纬度观察
old.par <- par(mfrow = c(1,2))
k = 2 # 根据上面的评估 k=2最优
clu <- kmeans(norm.data,k)
mds = cmdscale(dist(norm.data,method="euclidean"))
plot(mds, col=clu$cluster, main='kmeans聚类 k=2', pch = 19)
plot(mds, col=iris$Species, main='原始聚类', pch = 19)
par(old.par)

聚类完成后，有源原始数据是4纬，无法可视化，所以通过多维定标(Multidimensional scaling)将纬度将至2为，查看聚类效果，如下

 

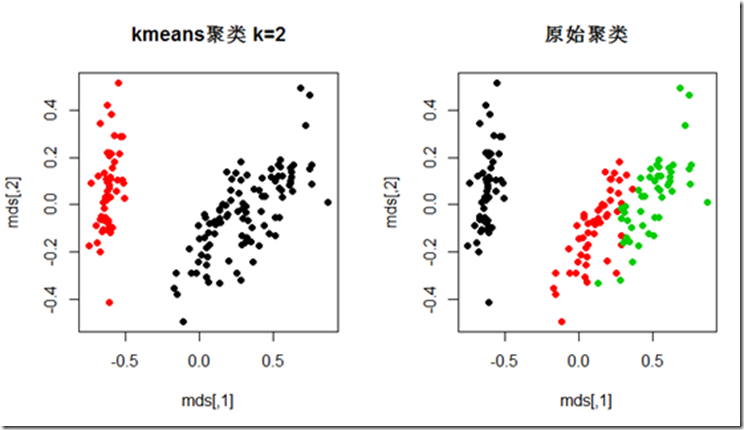
可以发现原始分类中和聚类中左边那一簇的效果还是拟合的很好的，右测原始数据就连在一起，kmeans无法很好的区分，需要寻求其他方法。

 

kmeans最佳实践

1. 随机选取训练数据中的k个点作为起始点

2. 当k值选定后，随机计算n次，取得到最小开销函数值的k作为最终聚类结果，避免随机引起的局部最优解

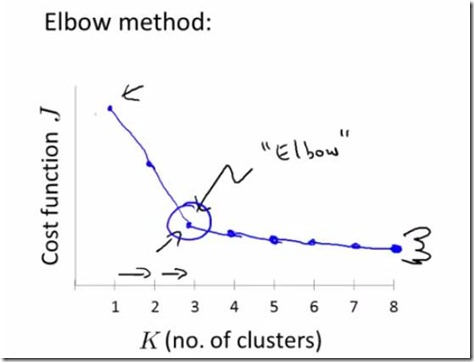
3. 手肘法选取k值：绘制出k--开销函数闪点图，看到有明显拐点（如下）的地方，设为k值，可以结合轮廓系数。

4. k值有时候需要根据应用场景选取，而不能完全的依据评估参数选取。

 

 

参考

[1] kmeans 讲义by Andrew NG

[2] 坐标下降法（Coordinate Decendent）

[3] 数据规格化

[4] 维基百科--轮廓系数

[5] kmeans算法介绍

[6] 降为方法—多维定标

[7] Week 8 in Machine Learning, by Andrew NG, Coursera