Chapter 3 Observational Studies

目录

• 概
• 3.1
• 3.2 Exchangeability
• 3.3 Positivity
• 3.4 Consistency
  • First
  • Second
• Fine Point
  • 3.1 Identifiability of causal effects
  • 3.2 Crossover randomized experiments
  • 3.3 Possible worlds
  • 3.4 Attributable fraction
• Technical Point
  • 3.1 Positivity for standardization and IP weighting
  • 3.2 Cheating consistency

Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.

概

这一章主要讨论的是, 观测得到的数据(而非随机实验)在什么条件下可以视为是随机试验.

outcome predictors: 一些会导致\(Y\)发生的诱因

3.1

1. 我们所考虑的\(A\)和实验中实际的采取的手段\(A\)是相一致的.

2. 采取何种手段\(A\)仅仅与\(L\)有关(这里考虑, \(L, A, Y\)三个元素).

3. \(\mathrm{Pr}(A|L) > 0\), 即正定性.

下面是一点一点的分析这三个点的重要性.

3.2 Exchangeability

这个对应的是第二点, 即我们要探究是否\(A\)仅仅与\(L\)有关, 从而有可交换性:

\[Y^a \amalg A |L.
\]

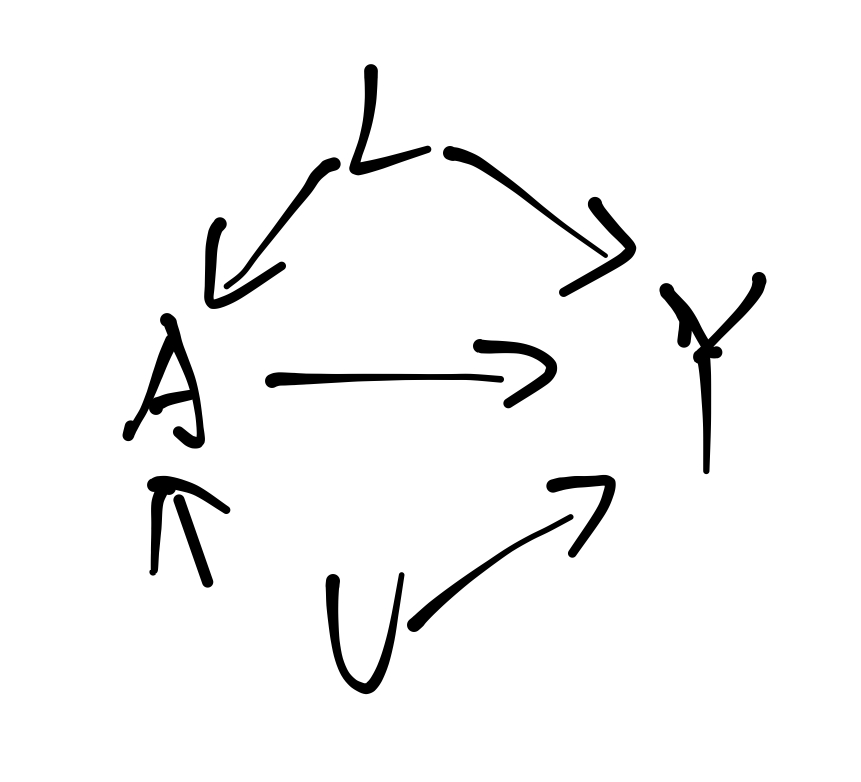
一旦遇到上面的情况, 往往就没有上述可交换性的保证了.

3.3 Positivity

设想\(L\)代表的是一个人是否吸烟, 倘若一个医生仅仅给不吸烟的人进行心脏迁移手术, 即

\[\mathrm{Pr}[A=1|L=1] = 0,
\]

则我们就完全丢失了这部分信息, 自然也没办法计算casual effect, 因为

\[\mathrm{Pr}[Y|A=1, L=1]
\]

压根没有定义.

3.4 Consistency

一致性分类预期结果的一致性, 以及结果和观测数据的一致性

First

现在假设\(A \in \{0, 1\}\), 即代表是否进行心脏移植手术, 但是在实际中, \(A\)并非如此纯粹的0, 1.

实际上, 取决于器材, 外科医生的差别会衍生出不同版本的\(A\).

当然了, 这么讨论下去只会导致不可知论, 我们可以在某种程度上假设, 不过对\(A\)的描述越细致, 即越细分, 最后的结论也会更加精准.

Second

这个一致性, 用公式就是

\[Y^a = Y, A=a,
\]

这个很重要, 因为我们在计算causal effect的时候有这么一步

\[\mathrm{Pr}[Y|A=a, L] = \mathrm{Pr}[Y^a|A=a, L].
\]

这个一致性, 个人的理解是, 我们所观察的\(A=a\)有很多版本, 可能与我们所希望的\(Y^a\)并不一致, 导致\(Y^a \not = Y\).

这里有一个微妙的东西, 实在是不知道如何描述了.

Fine Point

3.1 Identifiability of causal effects

指, 倘若不是随机实验, 我们需要一些额外的假设来得以计算causal effect.

3.2 Crossover randomized experiments

p32

这个讨论的是在不同的时间点\(t=0, t=1\).

3.3 Possible worlds

p35

3.4 Attributable fraction

p38

Technical Point

3.1 Positivity for standardization and IP weighting

p32

上一章讲了利用standardization 和 IP weighting 在条件可交换的假定下, 我们可以计算causal effect.

但是, 实际上这同时是需要positivity的假定的.

standardization:

\[\sum_l \mathbb{E} [Y|A=a, L=l] \mathrm{Pr} [L=l],
\]

这个式子需要\(\mathbb{E}[Y|A=a, L=l]\), 但是这个在某些\(P(A=a|L=l)=0\)的情况下是没有定义的.

另一方面, IP weighting

\[\mathbb{E} [\frac{I(A=a)Y}{f(A|L)}] = \mathrm{Pr}[L \in Q(a)]\sum_{l} \mathbb{E} [Y|A=a, L=l, L\in Q(a)] \mathrm{Pr} [L=l|L \in Q(a)],
\]

其中\(Q(a) = \{l; \mathrm{Pr} (A=a|L=l)>0\}\).

相当于, 认为地目标的集合缩小了.

里头还说, 上述的与

\[\mathbb{E} [\frac{I(A=a)Y}{f(a|L)}]
\]

不同, 而且说后者是undefined的, 可是后决定后者才是等价于上面所说的啊.

不过我倒是觉得无所谓的, 毕竟我们应该关心我们所关心的, 限定在\(f(a|L)\not = 0\)才是合适的区域.

3.2 Cheating consistency

p40