[BZOI2014]大融合——————线段树进阶

竟然改了不到一小时就改出来了， 可喜可贺

Description

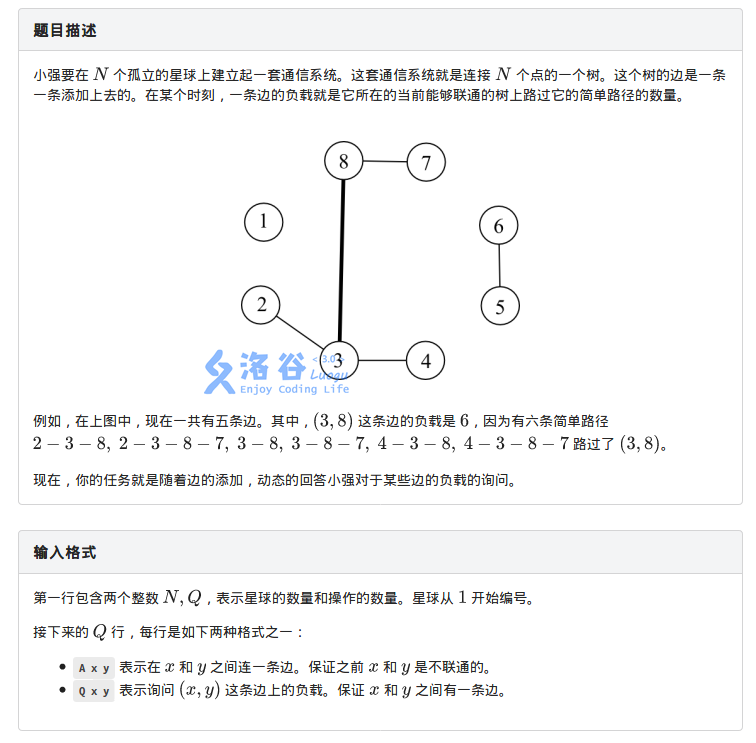
Solution

一开始想的是边两侧简单路径之和的乘积，之后发现这是个树形结构，简单路径数就是节点数。

之后的难点就变成了如何求线段树中不连续且无序区间中的权值。答案当然是没办法求

所以我们要进行离线，现将所有建边信息记录下来，把最终形成的树建好，然后在树上求DFS序。这样就能保证一个子树内的节点编号是连续的。

在查询时给出的两点一定具有父子关系，只需先找出二者中的儿子，之后求出它们所在树的节点树与儿子子树的节点树，做差后相乘即可。

CODE：

 1 #include<bits/stdc++.h>
 2 #define debug cout<<"lbwnb"
 3 using namespace std;
 4 const int NN=1e5+10;
 5 int siz[NN],dep[NN],lin[NN],tmp,to[NN*2],n,q,rt[NN],x,y,fa[NN],dat[NN][3],nex[NN*2],head[NN],num;
 6 char op[NN];
 7 inline void add(int a,int b){
 8     to[++num]=b;    nex[num]=head[a];    head[a]=num;
 9     to[++num]=a;    nex[num]=head[b];    head[b]=num;
10 }
11 inline int getf(int x){
12     return fa[x]==x?x:fa[x]=getf(fa[x]);
13 }
14 inline int read(){
15     int x=0,f=1;
16     char ch=getchar();
17     while(ch<'0'||ch>'9'){
18         if(ch=='-')    f=-1;
19         ch=getchar();
20     }
21     while(ch>='0'&&ch<='9'){
22         x=(x<<1)+(x<<3)+(ch^48);
23         ch=getchar();
24     }
25     return x*f;
26 }
27 void write(int x){
28     if(x<0)    putchar('-'), x=-x;
29     if(x>9)    write(x/10);
30     putchar(x%10+'0');
31 }
32 void dfs(int x){
33     lin[x]=++tmp;    siz[x]=1;
34     for(int i=head[x];i;i=nex[i]){
35         int v=to[i];
36         if(dep[v])    continue;
37         dep[v]=dep[x]+1;
38         dfs(v);
39         siz[x]+=siz[v];
40     }
41 }
42 struct node{
43     int ls[NN*40],rs[NN*40],seg,sum[NN*40];
44     void pushup(int x){
45         sum[x]=sum[ls[x]]+sum[rs[x]];
46     }
47     void insert(int &x,int l,int r,int pos,int val){
48         if(!x)    x=++seg;
49         if(l==r){ sum[x]+=val; return; }
50         int mid=(l+r)>>1;
51         if(pos<=mid)    insert(ls[x],l,mid,pos,val);
52         else    insert(rs[x],mid+1,r,pos,val);
53         pushup(x);
54     }
55     void merge(int &x,int y,int l,int r){
56         if(!x||!y){ x=x+y; return; }
57         if(l==r){ sum[x]+=sum[y]; return; }
58         int mid=(l+r)>>1;
59         merge(ls[x],ls[y],l,mid);
60         merge(rs[x],rs[y],mid+1,r);
61         pushup(x);
62     }
63     int query(int x,int l,int r,int opl,int opr){
64         if(l>=opl&&r<=opr)    return sum[x];
65         int mid=(l+r)>>1,ret=0;
66         if(opl<=mid)    ret+=query(ls[x],l,mid,opl,opr);
67         if(opr>mid)        ret+=query(rs[x],mid+1,r,opl,opr);
68         return ret;
69     }
70 }segt;
71 int main(){
72     n=read(); q=read();
73     for(int i=1;i<=q;i++)
74         cin>>op[i]>>dat[i][1]>>dat[i][2];
75     for(int i=1;i<=q;i++)
76         if(op[i]=='A')    add(dat[i][1],dat[i][2]);
77     for(int i=1;i<=n;i++)
78         if(!dep[i])    dep[i]=1,dfs(i);
79     for(int i=1;i<=n;i++)
80         segt.insert(rt[i],1,n,lin[i],1), fa[i]=i;
81      for(int i=1;i<=q;i++){
82         if(op[i]=='A'){
83             int r1=getf(dat[i][1]), r2=getf(dat[i][2]);
84             segt.merge(rt[r1],rt[r2],1,n);
85             fa[r2]=r1;
86         }
87          if(op[i]=='Q'){
88             int son=dep[dat[i][1]]>dep[dat[i][2]]?dat[i][1]:dat[i][2];
89             int ro=getf(dat[i][1]);
90             int tot=segt.query(rt[ro],1,n,1,n),sot=segt.query(rt[ro],1,n,lin[son],lin[son]+siz[son]-1);
91             write((tot-sot)*sot);    putchar('\n');
92         }
93     }
94     return 0;
95 }

I LOVE SEGMENT_TREE