【kafka学习笔记】合理安排broker、partition、consumer数量

broker的数量最好大于等于partition数量

一个partition最好对应一个硬盘，这样能最大限度发挥顺序写的优势。

broker如果免得是多个partition，需要随机分发，顺序IO会退化成随机IO。

实验条件：3个 Broker，1个 Topic，无Replication，异步模式，3个 Producer，消息 Payload 为100字节：

当 Partition 数量小于 Broker个数时，Partition 数量越大，吞吐率越高，且呈线性提升。

Kafka 会将所有 Partition 均匀分布到所有Broker 上，所以当只有2个 Partition 时，会有2个 Broker 为该 Topic 服务。3个 Partition 时同理会有3个 Broker 为该 Topic 服务。

当 Partition 数量多于 Broker 个数时，总吞吐量并未有所提升，甚至还有所下降。

可能的原因是，当 Partition 数量为4和5时，不同 Broker 上的 Partition 数量不同，而 Producer 会将数据均匀发送到各 Partition 上，这就造成各Broker 的负载不同，不能最大化集群吞吐量。

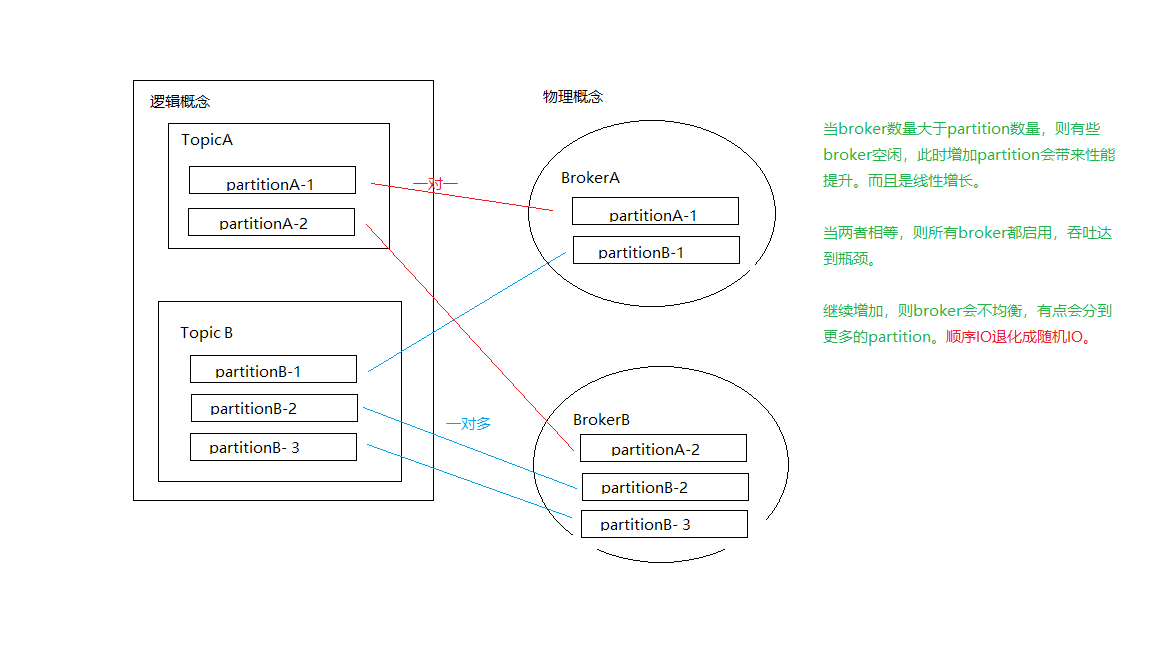
• 当broker数量大于partition数量，则有些broker空闲，此时增加partition会带来性能提升。而且是线性增长。

• 当两者相等，则所有broker都启用，吞吐达到瓶颈。

• 继续增加，则broker会不均衡，有点会分到更多的partition。

顺序IO退化成随机IO。

consumer数量最好和partition数量一致

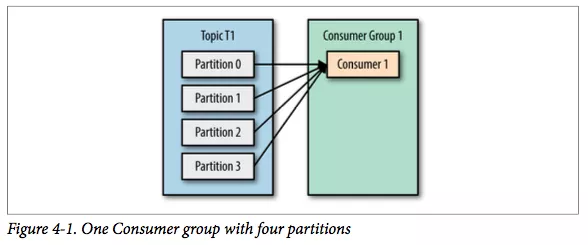
假设有一个 T1 主题，该主题有 4 个分区；同时我们有一个消费组 G1，这个消费组只有一个消费者 C1。

那么消费者 C1 将会收到这 4 个分区的消息。

如果我们增加新的消费者 C2 到消费组 G1，那么每个消费者将会分别收到两个分区的消息。

相当于 T1 Topic 内的 Partition 均分给了 G1 消费的所有消费者，在这里 C1 消费 P0 和 P2，C2 消费 P1 和 P3。

如果增加到 4 个消费者，那么每个消费者将会分别收到一个分区的消息。这时候每个消费者都处理其中一个分区，满负载运行。

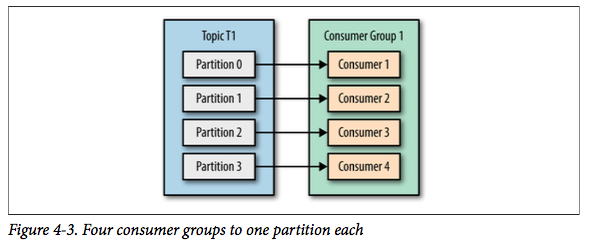
但如果我们继续增加消费者到这个消费组，剩余的消费者将会空闲，不会收到任何消息。

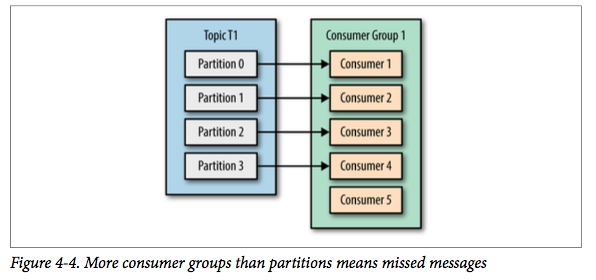
总而言之，我们可以通过增加消费组的消费者来进行水平扩展提升消费能力。这也是为什么建议创建主题时使用比较多的分区数，这样可以在消费负载高的情况下增加消费者来提升性能。

另外，消费者的数量不应该比分区数多，因为多出来的消费者是空闲的，没有任何帮助。如果我们的 C1 处理消息仍然还有瓶颈，我们如何优化和处理？

把 C1 内部的消息进行二次 sharding，开启多个 goroutine worker 进行消费，为了保障 offset 提交的正确性，需要使用 watermark 机制，保障最小的 offset 保存，才能往 Broker 提交。

● 保证顺序性，避免大的offest先提交，小的offest挂了，重启后会消息丢失。

● 解决：开一个协程专门提交offest，保证只提交最小的，重复消费代替消息丢失。

Kafka 一个很重要的特性就是，只需写入一次消息，可以支持任意多的应用读取这个消息。换句话说，每个应用都可以读到全量的消息。为了使得每个应用都能读到全量消息，应用需要有不同的消费组。

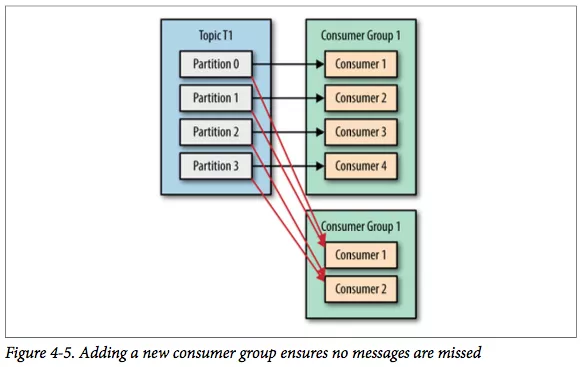
对于上面的例子，假如我们新增了一个新的消费组 G2，而这个消费组有两个消费者如图。在这个场景中，消费组 G1 和消费组 G2 都能收到 T1 主题的全量消息，在逻辑意义上来说它们属于不同的应用。

最后，总结起来就是：如果应用需要读取全量消息，那么请为该应用设置一个消费组；如果该应用消费能力不足，那么可以考虑在这个消费组里增加消费者。