Solution -「POI 2014」「洛谷 P5904」HOT-Hotels 加强版

\(\mathcal{Description}\)

  Link.

  给定一棵 \(n\) 个点的树，求无序三元组 \((u,v,w)\) 的个数，满足其中任意两点树上距离相等。

  \(n\le10^5\)。

\(\mathcal{Solution}\)

  考虑如何计数。对于任意三元组 \((u,v,w)\)，我们仅在其两两路径所进过的树上最高点对其统计一次。如图：

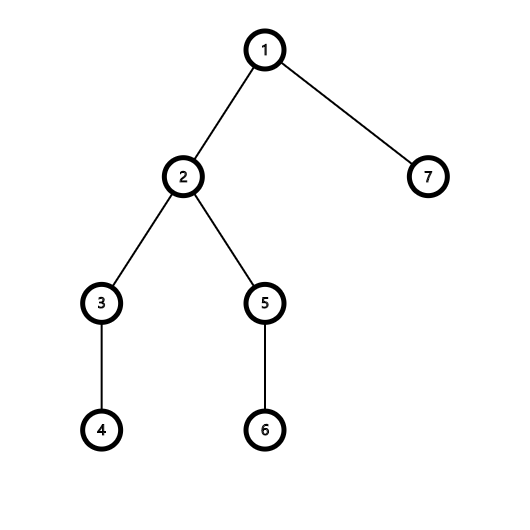
  对于三元组 \((4,6,7)\)，我们仅希望在 \(1\) 处统计它的贡献。

  考虑 DP，记 \(d(u,v)\) 表示 \(u\) 到 \(v\) 的树上距离。令 \(f(u,i)\) 表示 \(u\) 子树内 \(v\) 的个数，满足 \(d(u,v)=i\)；\(g(u,i)\) 表示 \(u\) 子树内无序二元组 \((p,q)\) 的个数，满足 \(d(p,\operatorname{lca}(p,q))=d(q,\operatorname{lca}(p,q))=d(\operatorname{lca}(p,q),u)+i\)。例如上图的 \(g(2,2)=1\)，无序二元组 \((4,6)\) 满足条件。

  如此设计状态的意义在于，在 \(g(u,i)\) 的基础上，在 \(u\) 子树的外部接上一个满足 \(d(u,w)=i\) 的 \(w\) 就能构成三元组，并且三元组恰好在最高点 \(u\) 计数。

  暴力转移比较显然，发现状态的第二维的范围均为 \(u\) 向下的最长链长，所以用长链剖分优化，直接移动指针继承 \(\mathcal O(1)\) 继承长儿子信息，做到均摊 \(\mathcal O(n)\) 转移，故总复杂度 \(\mathcal O(n)\)。

\(\mathcal{Code}\)

#include <cstdio>

#define alloc( u ) \
	( f[u] = cur, g[u] = ( cur += dep[u] << 1 ), cur += dep[u] << 1 )

typedef long long LL;

const int MAXN = 1e5;
int n, ecnt, head[MAXN + 5];
int dep[MAXN + 5], son[MAXN + 5];
LL ans, *f[MAXN + 5], *g[MAXN + 5], pool[MAXN * 5], *cur = pool;

struct Edge { int to, nxt; } graph[MAXN * 2 + 5];

inline void link ( const int s, const int t ) {
	graph[++ ecnt] = { t, head[s] };
	head[s] = ecnt;
}

inline void init ( const int u, const int fa ) {
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( ( v = graph[i].to ) ^ fa ) {
			init ( v, u );
			if ( dep[v] > dep[son[u]] ) son[u] = v;
		}
	}
	dep[u] = dep[son[u]] + 1;
}

inline void solve ( const int u, const int fa ) {
	if ( son[u] ) {
		f[son[u]] = f[u] + 1, g[son[u]] = g[u] - 1;
		solve ( son[u], u );
	}
	f[u][0] = 1, ans += g[u][0];
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( ( v = graph[i].to ) ^ fa && v ^ son[u] ) {
			alloc ( v ), solve ( v, u );
			for ( int j = 0; j < dep[v]; ++ j ) {
				if ( j ) ans += f[u][j - 1] * g[v][j];
				ans += g[u][j + 1] * f[v][j];
			}
			for ( int j = 0; j < dep[v]; ++ j ) {
				g[u][j + 1] += f[u][j + 1] * f[v][j];
				if ( j ) g[u][j - 1] += g[v][j];
				f[u][j + 1] += f[v][j];
			}
		}
	}
}

int main () {
	scanf ( "%d", &n );
	for ( int i = 1, u, v; i < n; ++ i ) {
		scanf ( "%d %d", &u, &v );
		link ( u, v ), link ( v, u );
	}
	init ( 1, 0 );
	alloc ( 1 );
	solve ( 1, 0 );
	printf ( "%lld\n", ans );
	return 0;
}