CF177A1/A2 Good Matrix Elements 题解

Content

给定一个 \(n\times n\) 的矩阵，每个元素都有一个值，求出处于两条对角线以及中间行和中间列的元素之和。

数据范围：\(1\leqslant n\leqslant 5(\text{A1})/100(\text{A2})\)。

Solution

前置知识：矩阵的主对角线即为左上到右下的对角线，副对角线即为左下到右上的对角线。

我们先观察处于题目中所要求的位置上的元素有哪些特征，以题目中给出的图为例：

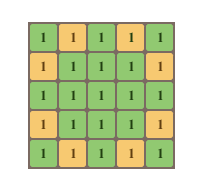
设元素的位置为 \((i,j)\)，我们发现，主对角线上的元素满足 \(i=j\)，副对角线上的元素满足 \(i+j=n+1\)，中间行的所有元素的行数都是 \(\left\lfloor\dfrac n2\right\rfloor+1\)，中间列的所有元素的列数都是 \(\left\lfloor\dfrac n2\right\rfloor+1\)。

因此，我们输入完 \(n\) 之后先把满足上述条件的所有元素的集合，也就是 \(\{(i,j)\mid i=j\text{ 或 }i+j=n+1\text{ 或 }i=\left\lfloor\dfrac n2\right\rfloor+1\text{ 或 }j=\left\lfloor\dfrac n2\right\rfloor+1\}\) 全部标记一下，输入每个元素的值的时候再把所有标记了的元素加进答案里面即可。

Code

int n, a[107][107], flag[107][107], ans;

int main() {
	n = Rint;
	F(i, 1, n) flag[i][i] = flag[i][n - i + 1] = flag[n / 2 + 1][i] = flag[i][n / 2 + 1] = 1;
	F(i, 1, n) F(j, 1, n) ans += flag[i][j] * (a[i][j] = Rint);
	return printf("%d", ans), 0;
}