数学图形之Kuen Surface

Kuen Surface应该又是一个以数学家名字命名的曲面.
本文将展示几种Kuen Surface的生成算法和切图,其中有的是标准的,有的只是相似.使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815

公式1

#http://jalape.no/math/kuentxt

vertices = D1: D2:

u = from  (-4.5) to (4.5) D1
v = from (PI*0.01) to (PI*0.99) D2

x=*(cos(u)+u*sin(u))*sin(v)/(+u*u*sin(v)*sin(v))
z=*(sin(u)-u*cos(u))*sin(v)/(+u*u*sin(v)*sin(v))
y=log(tan(v/))+*cos(v)/(+u*u*sin(v)*sin(v)) 

公式2

.

#http://www.mathcurve.com/surfaces/kuen/kuen.shtml

vertices = D1: D2:

u = from  (-4.5) to (4.5) D1
v = from (PI*0.01) to (PI*0.99) D2

x=*(cos(u)+u*sin(u))*sin(v)/(+u*u*sin(v))
z=*(sin(u)-u*cos(u))*sin(v)/(+u*u*sin(v))
y=ln(tan(v/))+*cos(v)/(+u*u*sin(v)) 

公式3

.

#http://www.mathcurve.com/surfaces/kuen/kuen.shtml

vertices = D1: D2:

u = from  (-4.5) to (4.5) D1
v = from (-PI*1.5) to (PI*1.5) D2

t = u*u+ch(v)*ch(v)

x=*(cos(u)+u*sin(u))*ch(v)/t
z=*(sin(u)-u*cos(u))*ch(v)/t
y=v - sh(*v)/t

公式4

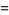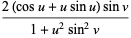			(1)
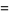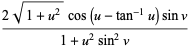			(2)
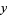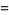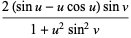			(3)
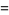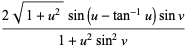			(4)

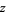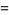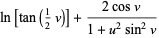#http://mathworld.wolfram.com/KuenSurface.html

vertices = D1: D2:

u = from  (-PI*1.6) to (PI*1.6) D1
v = from (PI*0.01) to (PI*0.99) D2

a = sin(u)
b = cos(u)
c = sin(v)
d = cos(v)

t =  + u*u*c*c

x = *(b + u*a)*c/t
z = *(a + u*b)*c/t
y = ln[tan(v/)] + *d/t

y = limit(y, -, )