HDU1254 推箱子（BFS） 2016-07-24 14:24 86人阅读 评论(0) 收藏

推箱子

Problem Description

推箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个M*N的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工只能推箱子而不能拉箱子,因此如果箱子被推到一个角上(如图2)那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.



现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.

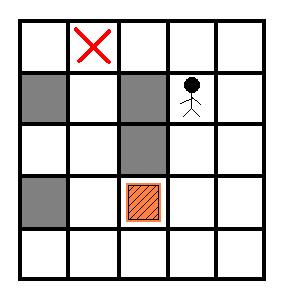
Input

输入数据的第一行是一个整数T(1<=T<=20),代表测试数据的数量.然后是T组测试数据,每组测试数据的第一行是两个正整数M,N(2<=M,N<=7),代表房间的大小,然后是一个M行N列的矩阵,代表房间的布局,其中0代表空的地板,1代表墙,2代表箱子的起始位置,3代表箱子要被推去的位置,4代表搬运工的起始位置.

Output

对于每组测试数据,输出搬运工最少需要推动箱子多少格才能帮箱子推到指定位置,如果不能推到指定位置则输出-1.

Sample Input

1
5 5
0 3 0 0 0
1 0 1 4 0
0 0 1 0 0
1 0 2 0 0
0 0 0 0 0

Sample Output

4

————————————————————————————————————————————

由于要求最小，所以用bfs记录箱子的移动，另外就是判断人能否到达位置，用bfs判断（也可以dfs）

开4维数组记录状态

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;

int dir[4][2] = { { -1, 0 }, { 0, 1 }, { 0, -1 }, { 1, 0 } };
int mp[10][10];
int vir[10][10][10][10];
int m, n;
struct node{
    int bx, by;
    int rx, ry;
    int cnt;
};
struct man{
    int x, y;
};

bool check(int i, int j)
{
    if (i<1 || i>m || j<1 || j>n || mp[i][j] == 1)
        return 0;
    return 1;
}

int bfs2(int si, int sj, int di, int dj, int bi, int bj)
{
    int vis[10][10];
    memset(vis, 0, sizeof(vis));
    queue<man>qu;
    man st, ed;
    st.x = si;
    st.y = sj;
    vis[si][sj] = 1;
    qu.push(st);
    while (!qu.empty())
    {
        st = qu.front();
        qu.pop();
        if (st.x == di&&st.y == dj)
            return 1;
        for (int i = 0; i < 4; i++)
        {
            ed.x = st.x + dir[i][0];
            ed.y = st.y + dir[i][1];
            if (check(ed.x, ed.y)&& !vis[ed.x][ed.y]&& (ed.x != bi||ed.y != bj))
            {
                vis[ed.x][ed.y] = 1;
                qu.push(ed);
            }
        }
    }
    return 0;
}

int bfs(int bi, int bj, int ri, int rj, int di, int dj)
{
    queue<node>q;
    node f, d;
    f.bx = bi;
    f.by = bj;
    f.rx = ri;
    f.ry = rj;
    f.cnt = 0;
    vir[bi][bj][ri][rj] = 1;
    q.push(f);
    while (!q.empty())
    {
        f = q.front();
        q.pop();
        if (f.bx == di&&f.by == dj)
            return f.cnt;
        for (int i = 0; i<4; i++)
        {
            d.bx = f.bx + dir[i][0];
            d.by = f.by + dir[i][1];
            d.rx = f.bx - dir[i][0];
                d.ry = f.by - dir[i][1];
            if (check(d.bx, d.by)&&check(d.rx,d.ry) && !vir[d.bx][d.by][d.rx][d.ry])
            {

                if (bfs2(f.rx, f.ry, d.rx, d.ry, f.bx, f.by))
                {
                    vir[d.bx][d.by][d.rx][d.ry] = 1;
                    d.cnt = f.cnt + 1;
                    q.push(d);
                }
            }
        }
    }
    return -1;
}

int main()
{
    int o, ri, rj, di, dj, bi, bj;
    scanf("%d", &o);
    while (o--)
    {
        scanf("%d%d", &m, &n);
        for (int i = 1; i<=m; i++)
        for (int j = 1; j<=n; j++)
        {
            scanf("%d", &mp[i][j]);
            if (mp[i][j] == 4)
            {
                ri = i;
                rj = j;
            }
            if (mp[i][j] == 2)
            {
                bi = i;
                bj = j;
            }
            if (mp[i][j] == 3)
            {
                di = i;
                dj = j;
            }
        }
        int ans = bfs(bi, bj, ri, rj, di, dj);
        memset(vir, 0, sizeof(vir));
        printf("%d\n", ans);

    }
    return 0;
}