fzyzojP3372 -- [校内训练20171124]博弈问题

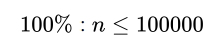
对于每个点都要答案

还是异或

trie树合并石锤了

朴素枚举是O(n^2*17)的

怎么办呢？

我们发现合并的时候，一些部分的trie的子树还是不变的

改变的部分也就是合并的复杂度可以接受

鉴于大部分trie都不变，而且是一个从上往下的过程，支持pushup维护

所以考虑dp，再在merge的pushup时候维护好dp值的更新

f[i]表示trie中以i为根子树，最后的游戏结果

转移分类讨论：

如果x的sz==1，令dp[x]=-1

否则如果仅x的某一个子树有sz，dp[x]=dp[son]

否则如果x的一个子树sz==1，那么先手一定选择这个子树，一定更优，那么后手的选择就固定了，就是在另一个子树trie上尽量使答案小。O(logn)转移一下

否则，那么先手进哪一个，后手一定跟进去，所以两个子树的dp取max即可

复杂度：O(nlog^2n)不严格

#include<bits/stdc++.h>
#define il inline
#define reg register int
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=+;
const int U=;//sudhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
int a[N];
struct node{
    int nxt,to;
}e[*N];
int hd[N],cnt;
int n;
void add(int x,int y){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
}
struct tr{
    int ls,rs;
    int sz,dp;
    int val;
}t[N*];
int tot;
int calc(int x,int d,int s){
    int ret=;
    int now=x;
    for(reg i=d+;i<=U;++i){
        int c=(s>>(U-i))&;
        if(c==){
            if(t[now].ls) now=t[now].ls;
            else now=t[now].rs,ret+=(<<(U-i));
        }else{
            if(t[now].rs) now=t[now].rs;
            else now=t[now].ls,ret+=(<<(U-i));
        }
    }
    return ret;
}
void pushup(int x,int d){
    t[x].sz=t[t[x].ls].sz+t[t[x].rs].sz;
    if(t[x].sz==) t[x].val=t[t[x].ls].val+t[t[x].rs].val;
    if(t[x].sz==){
        t[x].dp=-;
    }
    if(!t[t[x].ls].sz){
        t[x].dp=t[t[x].rs].dp;
    }else if(!t[t[x].rs].sz){
        t[x].dp=t[t[x].ls].dp;
    }else{
        if(t[t[x].ls].sz==){
            t[x].dp=calc(t[x].rs,d+,t[t[x].ls].val)+(<<(U-d-));
        }else if(t[t[x].rs].sz==){
            t[x].dp=calc(t[x].ls,d+,t[t[x].rs].val)+(<<(U-d-));
        }else{
            t[x].dp=max(t[t[x].ls].dp,t[t[x].rs].dp);
        }
    }
}
void upda(int &x,int d,int v){
    if(!x) x=++tot;
    //cout<<" xx "<<x<<" d "<<d<<" v "<<v<<endl;
    if(d==U){
        ++t[x].sz;
        t[x].val=v;
        if(t[x].sz==){
            t[x].dp=-;
        }else t[x].dp=;
        return;
    }
    if(v&(<<(U-d-)))// cout<<"is 1",
    upda(t[x].ls,d+,v);
    else //cout<<"is 0 ",
    upda(t[x].rs,d+,v);
    pushup(x,d);
}
int merge(int x,int y,int d){
    if(!x||!y) return x+y;
    if(d==U){
        t[x].sz+=t[y].sz;
        t[x].dp=;
        return x;
    }
    t[x].ls=merge(t[x].ls,t[y].ls,d+);
    t[x].rs=merge(t[x].rs,t[y].rs,d+);
    pushup(x,d);
    return x;
}
int rt[N];
int ans[N];
void dfs(int x,int fa){
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dfs(y,x);
        rt[x]=merge(rt[x],rt[y],);
    }
    //cout<<" x "<<x<<" "<<rt[x]<<" : "<<t[rt[x]].dp<<" "<<t[rt[x]].sz<<endl;
    upda(rt[x],,a[x]);
    ans[x]=t[rt[x]].dp;
}
int main(){
    rd(n);
    for(reg i=;i<=n;++i)rd(a[i]);
    int x,y;
    for(reg i=;i<n;++i){
        rd(x);rd(y);
        add(x,y);add(y,x);
    }
    dfs(,);
    for(reg i=;i<=n;++i){
        printf("%d\n",ans[i]);
    }
    return ;
}

}
signed main(){
    freopen("3372.in","r",stdin);
    freopen("3372.out","w",stdout);
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2019/2/3 17:19:49
*/

总结：

考虑在变化中寻找不变的，再进行维护

变化的毕竟在少数。

动态点分治就是这个思想。

要大胆DP

再认真分析维护的复杂度和方式。

也启示我们线段树不光是只能维护信息的存在与否。（其实都是靠pushup辣）