[洛谷P4492] [HAOI2018]苹果树

洛谷题目链接:[HAOI2018]苹果树

题目背景

HAOI2018 Round2 第一题

题目描述

小 C 在自己家的花园里种了一棵苹果树, 树上每个结点都有恰好两个分支. 经过细心的观察, 小 C 发现每一天这棵树都会生长出一个新的结点.

第一天的时候, 果树会长出一个根结点, 以后每一天, 果树会随机选择一个当前树中没有长出过结点 的分支, 然后在这个分支上长出一个新结点, 新结点与分支所属的结点之间连接上一条边.

小 C 定义一棵果树的不便度为树上两两结点之间的距离之和, 两个结点之间 的距离定义为从一个点走到另一个点的路径经过的边数.

现在他非常好奇, 如果 \(N\) 天之后小 G 来他家摘苹果, 这个不便度的期望 \(E\) 是多少. 但是小 C 讨厌分数, 所以他只想知道 \(E \times N !\) 对 \(P\) 取模的结果, 可以证明这是一个整数.

输入输出格式

输入格式：

从标准输入中读入数据. 一行两个整数 \(N\), \(P\) .

输出格式：

输出到标准输出中. 输出一个整数表示答案．

输入输出样例

输入样例#1：

3 610745795

输出样例#1：

24

输入样例#2：

305 1000000007

输出样例#2：

865018107

说明

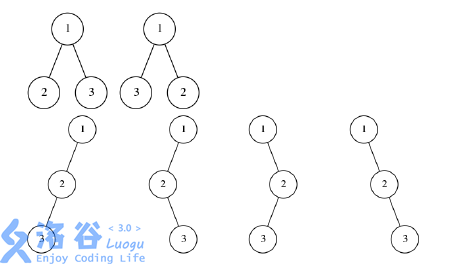
以上是所有 \(N = 3\) 时可能的苹果树形态, 其中编号表示这个结点是第几天生 长出来的, 显然每种情况两两结点的距离均为 \(4\) .

题解: 这个枚举方式比较神奇...我也不太清楚为什么可以做到不重不漏,有人会可以帮我分析一下...

直接讲方法吧:

首先考虑如何计算贡献,我们分每条边来计算贡献,那么总贡献就是\(\sum size*(n-size)\)

考虑当前枚举到了节点\(i\),它有一颗大小为\(j\)的子树,那么前\(i\)个节点可能组成的方案数是\(i!\),这个大小为\(j\)的子树的方案数有\(j!\)种,然后剩下的\(n-i-j\)个节点随便放,第一个节点可以放置的方案是\(i\)种,第二个是\(i+1\)种,那么剩下节点随便放的贡献就是\(\frac{(n-j)!}{(i-1)!}\),总贡献就是:$$\sum_{i=1}^{{n}\sum_{j=1}}{n-i}i!2C_{n-i}^jj!j(n-j)\frac{(n-j)!}{(i-1)!}$$

因为不一定存在逆元,可以先递推杨辉三角,然后把最后那部分用组合数乘阶乘的形式表示出来.

当然这题也有\(DP\)的解法,有兴趣可以自己看看别的题解

#include<bits/stdc++.h>
using namespace std;
const int N = 2000+5;

int n, mod, fac[N], c[N][N], ans = 0;

int main(){
    cin >> n >> mod; c[0][0] = fac[0] = fac[1] = 1;
    for(int i = 1; i <= n; i++){
        c[i][0] = 1;
        for(int j = 1; j <= n; j++) c[i][j] = (c[i-1][j]+c[i-1][j-1])%mod;
    }
    for(int i = 1; i <= n; i++) fac[i] = 1ll*fac[i-1]*i%mod;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n-i; j++)
            (ans += 1ll*fac[i]*2%mod*c[n-i][j]%mod*fac[j]%mod*j%mod*(n-j)%mod*c[n-j-1][n-i-j]%mod*fac[n-i-j]%mod) %= mod;
    cout << ans << endl;
    return 0;
}