主成分分析——PCA

在数据挖掘过程中，当一个对象有多个属性（即该对象的测量过程产生多个变量）时，会产生高维度数据，这给数据挖掘工作带来了难度，我们希望用较少的变量来描述数据的绝大多数信息，此时一个比较好的方法是先对数据进行降维处理。数据降维过程不是简单提取部分变量进行分析，这样的方式法当然会降低数据维度，但是这是非常不可取的方式（不专业一点，可以称之为“丢维”），违背了“降维”的含义。

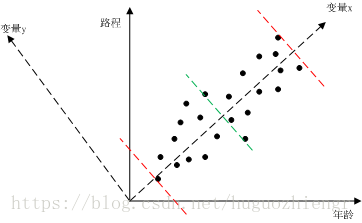
尽管我们并不确定不同变量之间是否一定有关系，但除非有确定的依据，我们最好还是猜测是有关系的，先看一个简单的例子，只有两个变量的情况。我们对人的年龄和他当前所走过的路程进行统计，然后绘制成图1（此处的例子是自己想的，不太妥当，只为说明问题）

​

图1

在图1中，我们对所有的样点进行一元线性回归分析，可以得到变量x直线，将变量x直线逆时针旋转90度，得到变量y直线（得到我们熟悉的二维直角坐标系），我们可以直观的看到样本数据主要沿着变量x分布，那么在数学上怎么去判别这种“直观的分布”呢？我们用最大方差来判别。图1中两条红色虚线是样本沿变量x的分布范围，绿色虚线是样本数据在变量x这一维度上的均值，这样我们就可以求得样本数据在变量x维度上的方差，类似的，可以求得样本数据在变量y上的方差，很明显，样本数据在变量x维度上的方差较大。

那么方差大说明什么问题呢？方差大说明样本数据在该维度上包含更多的信息。我们可以这样想，如果样本数据在某个维度上基本不变化，那么说明这个维度代表的变量的有、无对数据分布没有影响，该变量就没有存在的必要了，在测量过程中，我们就不必测量对象的这个属性。所以，此时可以用变量x这样一个变量来描述对象的年龄、路程属性。

这里还有两个问题需要说明，一个是变量x代表什么含义，另外一个就是在多维数据降维过程中，什么样的变量（类似于变量x这种）才是符合我们要求的变量。对于问题一，举个例子来说明Huba et al.(1981).收集了1684位洛杉矶学生消费13种合法和不合法兴奋性物质的数据，这些物质有：香烟、啤酒、红酒、酒精、可卡因、镇定剂、用于达到高潮的药房药剂、吗啡和其它鸦片制剂、大麻、麻药、吸入性麻醉剂、迷幻药和安非他明。Huba等人把使用药的情况定为：1（从未尝试），2（用过一次），3（用过几次），4（用过好多次），5（经常使用）。按照这些变量的顺序，得到的第一主成分为a，第二主成分为b。将a和b分别表示成原先13中变量（即13种兴奋性物质）的线性组合（没错，这里实际上就是用一组新的基去表示原样本数据矩阵，而我们可以用原变量去表示这一组新的基），得到a的权为（0.278，0.286，0.265，0.318，0.208，0.293，0.176，0.202，0.339，0.329，0.276,0.248,0.329），b的权为(0.280，0.396，0.392，0.325，-0.288，-0.259，-0.189，-0.315，0.163，-0.050，-0.169，-0.329，-0.232）.可以看到，成分a给每个变量的权值大致相等，因此我们可以认为a表示的含义是：衡量学生使用这些兴奋性物质的频繁程度，而对于成分b，它对于合法兴奋性物质的权值为正，而对于非法兴奋性物质的权值为负，因此可以认为b表示的含义为：当我们控制总体兴奋性物质的使用量，判断学生使用的兴奋性物质是合法还是非法的。对于问题二，在降维之后，我们会得到一系列的新的维度，以及这些维度所代表的变量，按照样本数据在这些维度上的投影所得数据的方差大小，对这些新的变量进行排列。假设我们选择前n个新的变量（假设有的话）,这n个新的变量就已经包含了原数据信息的90%，而这个比例也是我们能够接受的，那么这前n个变量就是满足我们需求的。

下面仔细说明降维的过程（为了方便，所有的向量这里我就不加方向箭头，只是标黑处理）

• 假设X是一个  的数据矩阵，行代表实例对象，列代表变量，我们先对每一列数据都去均值化，也即是列中数据都减去该列数据的均值（如果数据矩阵之前没有做过该处理）。我们关心的实际上是数据的变化情况，数据矩阵中每一个变量中的数值只是对变量的一种表示，表示的是具有变量所表示属性的不同实例对象间的相互关系（事实上我们可以对表示变量的数值做一系列变换，只要保持该变量的特性不变即可，例如大小、相等、加法、减法等），因此去均值后我们可以抛开测量过程带来的一些影响。
• 假设向量a是当X沿其投影时会使方差最大化的 列向量（也即时降维后满足我们要求的变量多表示的维），现在将数据矩阵X向向量a上投影，得到Xa，这是一个 的投影值列向量，我们对投影值列向量的方差定义为

                                                                                （1）

由于X的均值为0， V即为数据矩阵X的协方差矩阵。

• 在式（1）中，为了使得方差最大，我们可以对a各元素等比例放大，但是这是没有什么意义的，因此我们给a施加一个约束条件 —— a为单位向量，即,通过引入拉格朗日乘子法，我们得到下列最优化问题方程

对a进行求导，得到

这样就得到我们熟悉的特征值形式

                                                                   （2）

• 通过公式（2）我们可以求得一系列特征值  及其对应的特征向量  ,最大特征值对应的特征向量即为第一主成分分量，第二大特征值对应的特征向量即为第二主成分分量，以此类推。得到公式（2）后我们再回头看公式（1），方差即为，因此当我们选取前 k 个主成分分量来近似数据矩阵X时，可以对接近误差做如下定义

我们根据需要选取前k个主成分分量，并且使得接近误差在我们允许的范围内。