第八次作业-非确定的自动机NFA确定化为DFA
NFA 确定化为 DFA
子集法:
f(q,a)={q1,q2,…,qn},状态集的子集
将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合。
步骤:
1.根据NFA构造DFA状态转换矩阵
①确定DFA初态(NFA的所有初态集),字母表
②从初态出发,经字母表到达的状态集看成一个新状态
③将新状态添加到DFA状态集
④重复23步骤,直到没有新的DFA状态
2.画出DFA
3.看NFA和DFA识别的符号串是否一致。
练习:
1.解决多值映射:子集法
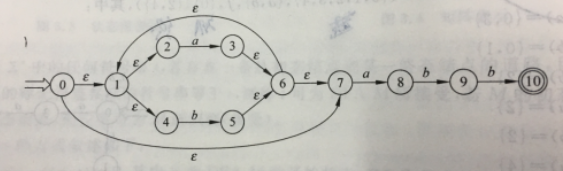
1). 发给大家的图1


2). P64页练习3
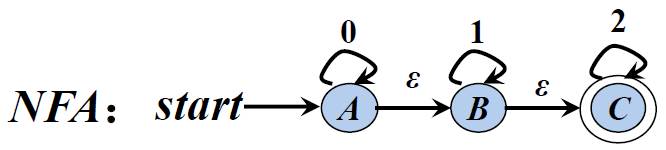
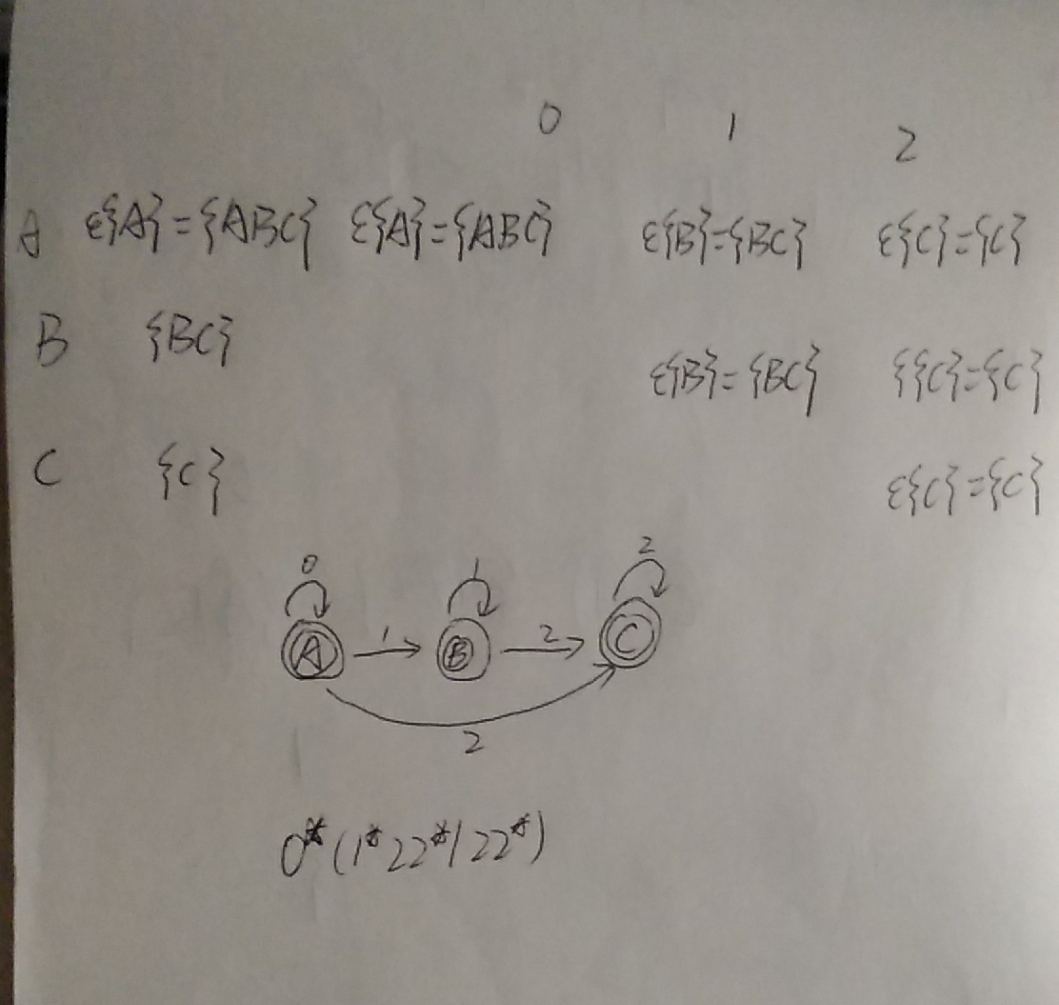
2.解决空弧:对初态和所有新状态求ε-闭包
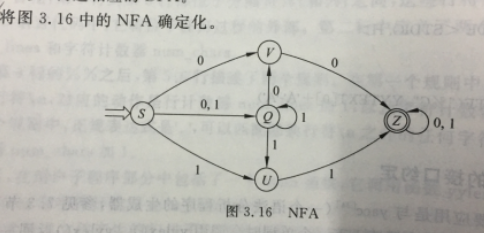
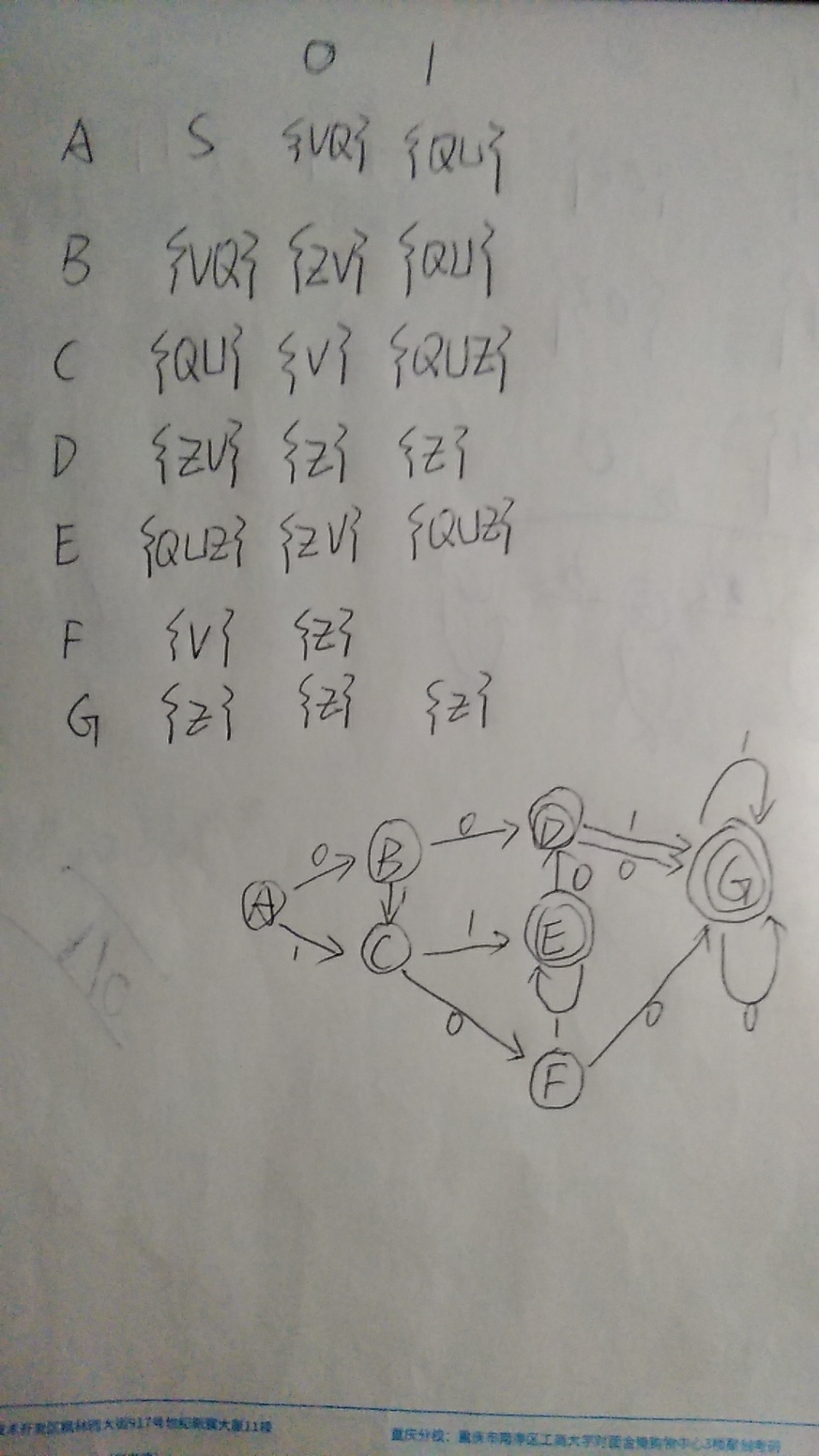
1). 发给大家的图2
2).P50图3.6

第八次作业-非确定的自动机NFA确定化为DFA的更多相关文章
- 第八次-非确定的自动机NFA确定化为DFA
提交作业 NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. ...
- 非确定的自动机NFA确定化为DFA
摘要: 在编译系统中,词法分析阶段是整个编译系统的基础.对于单词的识别,有限自动机FA是一种十分有效的工具.有限自动机由其映射f是否为单值而分为确定的有限自动机DFA和非确定的有限自动机NFA.在非确 ...
- 作业八——非确定的自动机NFA确定化为DFA
NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...
- 第八次——非确定的自动机NFA确定化为DFA
NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...
- 编译原理之非确定的自动机NFA确定化为DFA
1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1} f(0,b)={0} f(1,b)={2} f(2,b)={3} 画出状态转换矩阵 ...
- 编译原理:非确定的自动机NFA确定化为DFA
1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1} f(0,b)={0} f(1,b)={2} f(2,b)={3} 画出状态转换矩阵 ...
- 非确定有限状态自动机的构建(二)——将CharVal转换为NFA
保留版权,转载注明出处:潘军彪的个人博客(http://blog.csdn.net/panjunbiao/article/details/9378933) 将上下文无关文法读入内存之后,可以将它转换成 ...
- 非确定有限状态自动机的构建(一)——NFA的定义和实现
保留版权,转载需注明出处(http://blog.csdn.net/panjunbiao). 非确定有限状态自动机(Nondeterministic Finite Automata,NFA)由以下元素 ...
- oo第八次作业
oo第八次作业 第五次作业分析: 1.度量图: 2.类图: 第五次作业由于是第一次接触多线程,所以导致自己的经验不足,因此最终也没有完成作业,到最后任然不能实现三部电梯的有效调度,所以导致了这次作业的 ...
随机推荐
- Windows系统下搭建WAMP环境
Wamp就是Windos Apache Mysql PHP集成安装环境,即在window下的apache.php和mysql的服务器软件.其中php环境配置是至关重要的一部分,本文就针对php在本地的 ...
- Webpack 4 Tree Shaking 终极优化指南
几个月前,我的任务是将我们组的 Vue.js 项目构建配置升级到 Webpack 4.我们的主要目标之一是利用 tree-shaking 的优势,即 Webpack 去掉了实际上并没有使用的代码来减少 ...
- C++中对封装的语法支持——静态成员
静态成员(变量与函数) 1.静态成员变量的语法.访问.特点(共享.类内声明类外初始化) 静态成员变量在class中只做声明,并没有初始化所以不会分配内存. (1) 非静态成员变量必须通过对象来访问. ...
- NetCore基于EasyNetQ的高级API使用RabbitMq
一.消息队列 消息队列作为分布式系统中的重要组件,常用的有MSMQ,RabbitMq,Kafa,ActiveMQ,RocketMQ.至于各种消息队列的优缺点比较,在这里就不做扩展了,网上资源很多. 更 ...
- Python3.7.1学习(七)mysql中pymysql模块详解(一)
pymysql是纯用Python操作MySQL的模块,其使用方法和MySQLdb几乎相同.此次介绍mysql以及在python中如何用pymysql操作数据库, 以及在mysql中存储过程, 触发器以 ...
- 【Flume】Flume基础之安装与使用
1.Flume简介 (1) Flume提供一个分布式的,可靠的,对大数据量的日志进行高效收集.聚集.移动的服务,Flume只能在Unix环境下运行. (2) Flume基于流式架构,容错性强, ...
- bash:裁剪字符串 ${var:3:2}
1)按照index和长度裁剪变量字符串var=foobar echo ${var:3} -------bar echo ${var:3:2} -------ba 从index为3开始,取两个echo ...
- windows 通过appache链接cgi程序
#!D:\Python27\ print 'Content-type: text/plain' print print 'Hello, world' 出现错误 The server encounter ...
- firefox浏览器window.event is undefined问题
获取鼠标坐标,IE下window.event.clientX和window.event.clientY就可以获取x,y的座标了.但是firefox却不行,浏览器报错window.event is un ...
- 【目标检测实战】目标检测实战之一--手把手教你LMDB格式数据集制作!
文章目录 1 目标检测简介 2 lmdb数据制作 2.1 VOC数据制作 2.2 lmdb文件生成 lmdb格式的数据是在使用caffe进行目标检测或分类时,使用的一种数据格式.这里我主要以目标检测为 ...
