提升——树形DP

这里讲提高一点的内容，所以没有树形DP基础的，先看一下基础部分：

浅说——树形DP

闲言不表，看第一题。

这道题是典型的树上最长链问题。（就是一个模板题）

给定一棵树，树上共有N个节点(N<=5000) ，树上节点的编号从1到N，每个节点的儿子个数最多为N-1。

请求出这棵树上的经过节点数最多的一条不重复的链。

输入： 第一行一个数N，表示树有N个节点。 接下来N行，每行第一个数为Xi(0<=Xi<=N-1),表示编号为i的节点的儿子个数为Xi,接下来Xi个数，依次表示每一个儿子的编号。Xi为0表示没有儿子。

输出： 一行一个数，表示最长链经过的节点个数。 （内存限制10M）

样例输入：

样例输出：

问题分析：

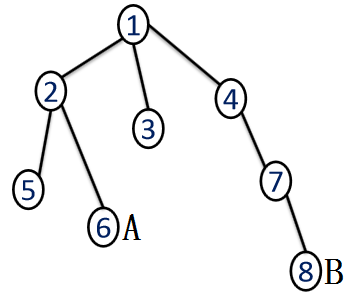
目标：如图计算1为根的树上最长链

动机：通过分析子树的相关信息，算出目标值

分析有两种情况：

一、最长链不经过1号节点.

这种情况下，找到的点A一定是最长链的一个端点。

由于1是最长链上的点，那么最长链的另一个端点到T的距离是一定的，因此A到T必定要取最长的距离，该链才能最长。此种情况容易理解，不加赘述。

二、最长链经过1号节点。

若T不在最长链上，则最长链必定在T的一个子树中。上图中最长链就在以C为根的子树中。

那么我们可以下一个结论：找到距离T最远的一个点A，那么A必定是最长链的一个端点，且从A到T的路径必定与最长链重合从A到C的这一段。

下面我们来证明结论：

假设T的最长链在子树C中，且子树C中最深的节点A对于根节点T的深度为h(A)。如果距离T最远的某个节点P不在子树C中，那么P-T-C-A的长度一定大于子树C中最长链的长度，与T中最长链在子树C中的条件矛盾。所以A必为最长链的一个端点，然后再一次搜索找到距离

A最远的节点B，AB即为最长链。

持续更新中……