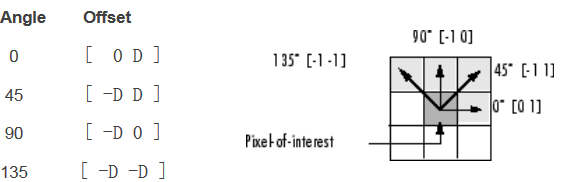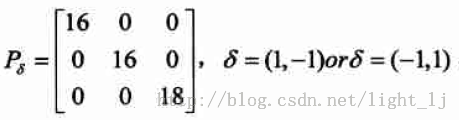灰度共生矩阵（Gray-level Co-occurrence Matrix，GLCM），矩阵的特征量

又叫做灰度共现矩阵

Prerequisites

概念

计算方式

对于精度要求高且纹理细密的纹理分布，我们取像素间距为d=1d=1，以下是方向的说明：

我们来看，matlab内置工具箱中的灰度共生矩阵的生成函数graycomatrix（gray-level co-occurrence matrix）对方向的说明：

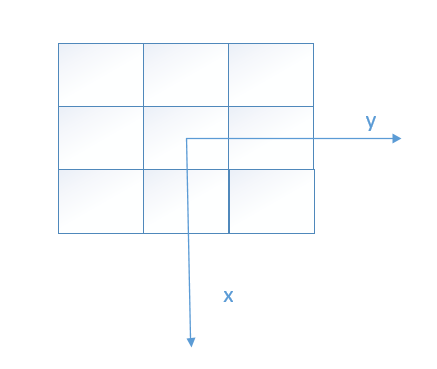
如上图所示，方向是在每一个像素点（pixel of interest）的邻域（当然，边界点除外）中获得的，只不过这里的坐标系变为了：

• δ=(0,±1)δ=(0,±1)为水平方向扫描，也即θ=0∘orθ=180∘θ=0∘orθ=180∘；
• δ=(±1,0)δ=(±1,0)为垂直扫描（θ=90∘orθ=−90∘θ=90∘orθ=−90∘）；
• δ=(1,−1),δ=(−1,1)δ=(1,−1),δ=(−1,1)是−45∘−45∘或135∘135∘扫描；
• δ=(1,1),δ=(−1,−1)δ=(1,1),δ=(−1,−1)是45∘45∘扫描。

一旦像素间距离dd以及像素间空间位置关系δδ确定，即可生成灰度共生矩阵。

GLCM所表示的是纹理图像的某些统计特性，所谓统计，通俗地讲就是累计某种情况出现的次数，用这一次数除以总的情况数，即可得其统计意义上的概率。

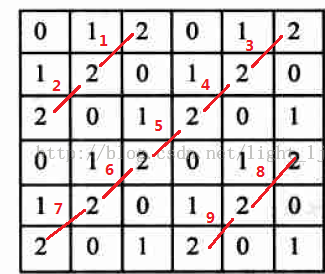
我们来统计灰度级2与2在-45度和135度方向上（也即δ=(1,−1)δ=(1,−1)或者δ=(−1,1)δ=(−1,1)）出现的次数，如图所示，共出现九次，在两个方向上即是18次。

matlab

matlab相关工具箱函数

使用灰度共生矩阵（GLCM）描述和提取图像纹理特征，是一个强大且流行的工具，自然matlab工具箱会提供相应的函数——graycomatrix：

给出一个图像矩阵，设置一些参数，得到其灰度共生矩阵，这就是函数的基本用法：

[glcm, SI] = graycomatrix(I, ...)

• 1

主要的参数有二个，分别是

1. NumLevels（灰度级数）

最终glcm的size是NumLevels*NumLevels

1. Offset（方向[0, 1; -1, 1; -1, 0; -1, -1]）：

[0, 1]中的1表示的偏移数（offset），当然也可以取2或者更多，如上文所说，对于精度要求高且图像纹理本身即很丰富的图像来说，为了更精细地刻画，我们取偏移量（offset）为1。

我们将原始I转换为SI，对SI计算GLCM，SI中元素的值介于[1, NumLevels]之间。

I = [
    1 1 5 6 8 8;
    2 3 5 7 0 2;
    0 2 3 5 6 7
    ];

[glcm, SI] = graycomatrix(I, 'NumLevels', 9, 'G', [])
% 'Offset'的default值为`[0, 1]`

glcm =

     0     0     2     0     0     0     0     0     0
     0     1     0     0     0     1     0     0     0
     0     0     0     2     0     0     0     0     0
     0     0     0     0     0     2     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     2     1     0
     0     0     0     0     0     0     0     1     1
     1     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     1

SI =

     2     2     6     7     9     9
     3     4     6     8     1     3
     1     3     4     6     7     8

demo

这里先写一个demo，稍微有点难懂的地方在于灰度共生矩阵的计算方式，然后是一些编程上的循环判断。其他方向的情况还未考虑（在第三和第四层循环的地方可能会略有不同），以及将其封装成一个函数的操作还是留待以后吧：

clear, clc
P = [ 0 1 2 0 1 2
   1 2 0 1 2 0
   2 0 1 2 0 1
   0 1 2 0 1 2
   1 2 0 1 2 0
   2 0 1 2 0 1];
[r, c] = size(P);
P_u = unique(P);        % 去重，得到所有的灰度级
n = length(P_u);        % 不同灰度级的个数
G = zeros(n, n);        % 初始化灰度共生矩阵为全0矩阵，

%% 四层循环，最外层的两层循环用来为GLCM的各个位置赋值
% 内层的两层循环时遍历原始图像矩阵，累计符合某一对应关系的的情况出现的次数

for p = 1:n,
    for q = 1:n,

        cnt = 0;            % GLCM刻画的是灰度图像像素的统计特性，在matlab中通过次数的统计计算得到
        for i = 1:r,
            for j = 1:c,
                if  (j+1) <= c && ((P(i, j) == p && P(i, j+1) == q) || P(i, j) == q && P(i, j+1) == p),
                    cnt = cnt + 1;
                end
            end
        end
        G(p, q) = cnt;
    end
end
G

References

[1] <图像特征提取——灰度共生矩阵（GLCM）>

版权声明：本文为博主原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/lanchunhui/article/details/49903791

---

矩阵的特征量：
从灰度共生矩阵上可以简单的看出，如果对角附近的元素有较大的值，说明图像的像素具有相似的像素值，如果偏离对角线的元素会有比较大的值，说明像素灰度在局部有较大变化。为了得到更多的纹理特征，我们还需要在进行计算：

对比度）（或反差）（contrast）：

纹理沟纹越深，其对比度越大，视觉效果越清晰；反之，对比度小，则沟纹浅，效果模糊。灰度差即对比度大的象素对越多，这个值越大。灰度公生矩阵中远离对角线的元素值越大，con越大。所以con越大图像越清晰

相关度（inverse different moment）：

度量空间灰度共生矩阵元素在行或列方向上的相似程度，因此，相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时，相关值就大;相反，如果矩阵像元值相差很大则相关值小。

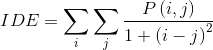
能量：是灰度共生矩阵元素值的平方和，所以也称之为能量，反映了图像灰度分布均匀程度和纹理粗细度。ASM值大表明一种较均一和规则变化的纹理模式。

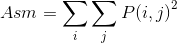
熵（entropy）：熵在物理中的含义就是物体的规则度，越有序熵越小，越无序熵越大。此处熵同样表示图像的信息量，当共生矩阵中所有元素有最大的随机性、空间共生矩阵中所有值几乎相等时，共生矩阵中元素分散分布时，熵较大。它表示了图像中纹理的非均匀程度或复杂程度。

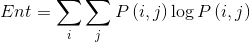
自相关（correlation）：反应了图像纹理的一致性。如果图像中有水平方向纹理，则水平方向矩阵的COR大于其余矩阵的COR值。

补充：
当灰度级较大时，是一个庞大的矩阵。对于一般的灰度图，灰度级就有256，那么中就有个元素，如此庞大的矩阵会使后续的计算量增加，所以灰度共生矩阵一般要经过处理以减少灰度级数，比如通过分析纹理图像直方图，在不影响图像纹理质量的前提下，经过适当的变换压缩灰度级。

参考：

《数字图像处理与计算机视觉：visual C++与Matlab实现》章挣
————————————————
版权声明：本文为CSDN博主「light_lj」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/light_lj/article/details/26098815