题解报告：poj 3233 Matrix Power Series（矩阵快速幂）

Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1

Sample Output

1 2
2 3
解题思路：等比矩阵求和，采用递归二分的方法。

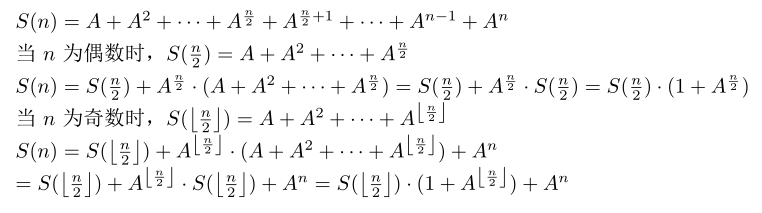
上图就给出了求前k项等比矩阵的和的递推式，解法采用递归来求和比较直观，也很好理解。
AC代码(1704ms)：

 #include<iostream>
 #include<cstring>
 using namespace std;
 const int maxn=;
 int n,k,mod;
 struct Matrix{int m[maxn][maxn];}init;
 Matrix add(Matrix a,Matrix b){//矩阵加法
     Matrix c;
     for(int i=;i<n;++i)
         for(int j=;j<n;++j)
             c.m[i][j]=(a.m[i][j]+b.m[i][j])%mod;
     return c;
 }
 Matrix mul(Matrix a,Matrix b){//矩阵乘法
     Matrix c;
     for(int i=;i<n;i++){
         for(int j=;j<n;j++){
             c.m[i][j]=;
             for(int k=;k<n;k++)
                 c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
         }
     }
     return c;
 }
 Matrix quick_power(Matrix a,int x){//矩阵快速幂
     Matrix b;memset(b.m,,sizeof(b.m));
     for(int i=;i<n;++i)b.m[i][i]=;//单位矩阵
     while(x){
         if(x&)b=mul(b,a);
         a=mul(a,a);x>>=;
     }
     return b;
 }
 Matrix sum(Matrix s,int k){//求前k项和
     if(k==)return s;//递归出口：当幂指数为1时，返回当前的矩阵
     Matrix tmp;memset(tmp.m,,sizeof(tmp.m));//暂存保存中间的矩阵
     for(int i=;i<n;++i)tmp.m[i][i]=;//单位矩阵
     tmp=add(tmp,quick_power(s,k>>));//计算1+A^{k/2}
     tmp=mul(tmp,sum(s,k>>));//计算(1+A^{k/2})*(A + A^2 + A^3 + … + A^{k/2})=(1+A^{k/2})*(S_{k/2})
     if(k&)tmp=add(tmp,quick_power(s,k));//若k是奇数，则加上A^k
     return tmp;//返回前k项的值
 }
 void print_rectangle(Matrix r){
     for(int i=;i<n;++i)
         for(int j=;j<n;++j)
             cout<<r.m[i][j]<<((j==n-)?"\n":" ");
 }
 int main(){
     while(cin>>n>>k>>mod){
         for(int i=;i<n;++i)
             for(int j=;j<n;++j)
                 cin>>init.m[i][j];
         init=sum(init,k);
         print_rectangle(init);
     }
     return ;
 }

采用分块矩阵求解可以减少很多时间，具体推导可以结合下图：

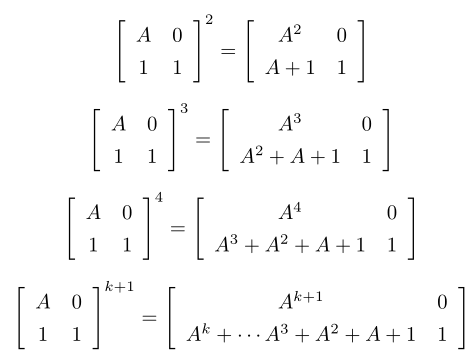
矩阵中套矩阵，效率上比上一种方法更快，实际上是2n×2n的矩阵快速幂。就样例展开等式左边的矩阵：

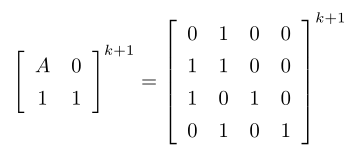
那么最终的答案就是等式右边矩阵中左下角的子矩阵减去单位矩阵，注意某个元素值减-1之后可能为-1，那么此时只需再加上mod即可。

AC代码(610ms)：

 #include<iostream>
 #include<cstring>
 using namespace std;
 const int maxn=;
 struct Matrix{int m[maxn][maxn];}init;
 int n,k,mod;
 Matrix mul(Matrix a,Matrix b){//矩阵乘法
     Matrix c;
     for(int i=;i<*n;i++){//矩阵大小扩大两倍，枚举第一个矩阵的行
         for(int j=;j<*n;j++){//枚举第二个矩阵的列
             c.m[i][j]=;
             for(int k=;k<*n;k++)//枚举第一个矩阵的列
                 c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
         }
     }
     return c;
 }
 Matrix POW(Matrix a,int x){//矩阵快速幂
     Matrix b;memset(b.m,,sizeof(b.m));
     for(int i=;i<*n;++i)b.m[i][i]=;//构造单位矩阵
     while(x){
         if(x&)b=mul(b,a);
         a=mul(a,a);x>>=;
     }
     return b;
 }
 void print_rectangle(Matrix r){
     for(int i=;i<n;++i){
         for(int j=;j<n;++j){
             if(i==j)r.m[n+i][j]-=;
             if(r.m[n+i][j]<)r.m[n+i][j]+=mod;//左下角子矩阵减去单位矩阵，减完可能小于0，因此需要加上mod再取余mod
             cout<<r.m[n+i][j]<<((j==n-)?'\n':' ');
         }
     }
 }
 int main(){
     while(cin>>n>>k>>mod){
         memset(init.m,,sizeof(init.m));//全部初始化为0
         for(int i=;i<n;++i){//首先初始化矩阵
             for(int j=;j<n;++j)
                 cin>>init.m[i][j];
             init.m[n+i][i]=init.m[n+i][n+i]=;//其余是单位矩阵
         }
         init=POW(init,k+);//求其前k+1项和（左下角包含单位矩阵，最后输出要减去单位矩阵）
         print_rectangle(init);//打印等比矩阵A前k项和
     }
     return ;
 }