bzoj 4316: 小C的独立集【仙人掌dp】

参考：https://www.cnblogs.com/clrs97/p/7518696.html

其实和圆方树没什么关系

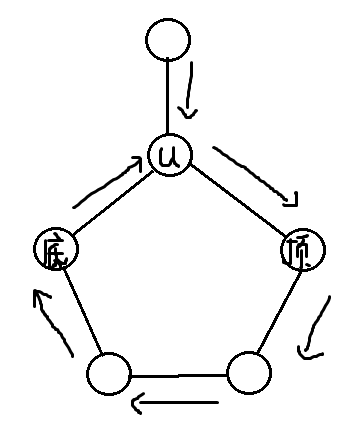
设f[i][j][k]为i点选/不选，这个环的底选不选

这个底的定义是设u为这个环在dfs中第一个被扫到的点，箭头表示dfs序：

#include<iostream>
#include<cstdio>
using namespace std;
const int N=100005;
int n,m,h[N],cnt,in[N],dfn,fa[N],f[N][2][2],a[2][2],ans;
bool tp[N],bt[N];
struct qwe
{
	int ne,to;
}e[N<<1];
int read()
{
	int r=0,f=1;
	char p=getchar();
	while(p>'9'||p<'0')
	{
		if(p=='-')
			f=-1;
		p=getchar();
	}
	while(p>='0'&&p<='9')
	{
		r=r*10+p-48;
		p=getchar();
	}
	return r*f;
}
void add(int u,int v)
{
	cnt++;
	e[cnt].ne=h[u];
	e[cnt].to=v;
	h[u]=cnt;
}
void dfs(int u,int fat)
{
	in[u]=++dfn;
	fa[u]=fat;
	for(int i=h[u];i;i=e[i].ne)
		if(e[i].to!=fat&&in[e[i].to])
			bt[u]=1;
	f[u][1][bt[u]]=1;
	for(int i=h[u];i;i=e[i].ne)
		if(e[i].to!=fat)
		{
			if(!in[e[i].to])
			{
				dfs(e[i].to,u);
				a[0][0]=a[0][1]=a[1][0]=a[1][1]=0;
				for(int j=0;j<2;j++)
					for(int k=0;k<2;k++)
						for(int p=0;p<2;p++)
							if(!j||!p)
								for(int q=0;q<2;q++)
									if(!tp[e[i].to]||!j||!q)
										a[j][k|(q&!tp[e[i].to])]=max(a[j][k|(q&!tp[e[i].to])],f[u][j][k]+f[e[i].to][p][q]);
				for(int j=0;j<2;j++)
					for(int k=0;k<2;k++)
						f[u][j][k]=a[j][k];
			}
			else if(in[e[i].to]<in[u])
			{
				int x=u;
				while(fa[x]!=e[i].to)
					x=fa[x];
				tp[x]=1;
			}
		}
}
int main()
{
	n=read(),m=read();
	for(int i=1;i<=m;i++)
	{
		int x=read(),y=read();
		add(x,y),add(y,x);
	}
	for(int i=1;i<=n;i++)
		if(!in[i])
		{
			dfs(i,0);
			int nw=0;
			for(int j=0;j<2;j++)
				for(int k=0;k<2;k++)
					nw=max(nw,f[i][j][k]);
			ans+=nw;
		}
	printf("%d\n",ans);
	return 0;
}