洛谷——P1229 遍历问题

P1229 遍历问题

题目描述

我们都很熟悉二叉树的前序、中序、后序遍历，在数据结构中常提出这样的问题：已知一棵二叉树的前序和中序遍历，求它的后序遍历，相应的，已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序遍历，你却不能确定其中序遍历序列，考虑如下图中的几棵二叉树：

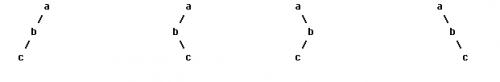
所有这些二叉树都有着相同的前序遍历和后序遍历，但中序遍历却不相同。

我们知道前序遍历和后序遍历不能确定出一颗唯一的二叉树，那么无论儿子放左边还是放右边都不会影响遍历顺序，那么问题就转化为求只有一个儿子的父节点，根据乘法原理，答案为

$x$为只有一个儿子的父节点个数，$ans=x^2$

#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;

string s1,s2;
int ans;

int main()
{
    cin>>s1>>s2;
    int l1=s1.length(),l2=s2.length();
    for(int i=;i<l1;i++){
        for(int j=;j<l2;j++){
            if(s1[i]==s2[j]&&s1[i+]==s2[j-]){
                ++ans;
            }
        }
    }

    printf("%d",<<ans);

    return ;
}