python 下的数据结构与算法---1：让一切从无关开始

这段时间把《Data Structure and Algorithms with python》以及《Problem Solving with  Algorithms and DataStructures》看完了（图那部分没仔细看，毕业设计开始了，有点忙）。现在开始写点总结啦，主要顺序按照是problem solving那本书的，感觉这本条理更加清晰简单，而另一本相对杂乱些，不过其代码写的更pythonic一些。【github地址，包含了那两本书带笔记版以及下面零的代码】

这作为第一篇总结笔记就从点无关的开始吧（也就是这两本书中提到的python相关但是与数据结构和算法无关的东东）【此后我尽量每天晚上更新一篇】

目录：

零：有些什么东西

一：几句对于python的闲语总结

二：python的赋值语句会发生什么

三：类的两种方法：访问方法与突变方法

四：python的变量查找机制

五：python程序运行内存机制

*六：运算符重载&类的内建方法

 零：有些什么东西：

一：几句对于python的闲语总结：

　　Python为解释性语言,用解释器（interpreter）运行

　　Python为动态语言，程序中不需要固定变量类型，同一个变量前后可以调用不同类型。

　　Python为面对对象语言，其所有的数据结构都是对象。（注：若看文档遇到Type，其实就是表示class，type是元类，用于构建类。x.__class__.__class__）

二：python的赋值语句会发生什么

赋值语句：x = 6

其实这个过程是建立了一个指向（reference），左边的是指向，右边的是一个对象（object）或者一个有指向对象的指向，可以有多个指向指向同一个对象（object）,[注意此地对象的意思，可以是值，实例，函数等等]，

综上，此地时建立了一个叫x的变量（variable）让其拥有object 6的reference

注意：

>>> a=[1,2,3,4]

>>> b=a

>>> a[0]=None

>>> b

[None, 2, 3, 4]

此地可以看出，其实指向就是指向了物理地址的一堆东西，一变都变。

三：类的两种方法

所有面对对象语言中都有两种方法：

　　访问方法（accessor method）与突变方法（mutator method）

访问方法取得对象来用但是不改变对象，而突变方法就是改变对象:

>>> a[::-1]

[5, 4, 3, 2, 1]

>>> a

[1, 2, 3, 4, 5]

>>> a.reverse()

>>> a

[5, 4, 3, 2, 1]

其实自己写过类就能够发现这两种的不同，大概访问方法就是用来return一些想要的值的，突变方法是用来改变对象内容的，一般也可以不return。

一个类如果没有访问方法那就是只能放数据不能取数据，那没什么意义。而一个类如果没有突变方法那就是不可变数据了，str，int等等数据类型就是这样的。

四：python的变量查找机制

　　python变量查找最先分为两步：首先在local scope查找，如绿色的val，先在绿色区域查找，没有再在encloding scope查找，即是浅红色区域

　　前面说到了local scope与enclosing scope，其实我们最熟的是global scope，即全局变量

　　用法：

　　x=0

　　def aha():

　　global  x

　…

　　最后有python的Build-in scope:

　　　　例如在函数中写了x=int(‘6’),

　　　　会依次寻找对象int函数是否在local scope，enclosing scope，

　　　　Global scope，最后看build-in scope

　　总结起来就是LEGB的查找顺序。

五：python的内存机制

　　从中也可以看出其实每个函数或者类都有个自己的内存空间，其实python在运行时，将使用两部分来运行，其都是在RAM（随机存储器）中的，两部分就是一个heap（堆）以及一个run-time stack（时间运行堆），当python解释器（interpreter）执行到某个函数是，将其对应的Activation Record压入run-time stack并且开辟一段新的scope，注意，所有local scope拥有的object都存储在Heap中，Activation Record中有他们的references，一旦函数执行完成，Activation Record弹出，下一个进入时会指向另一段scope。【见下图】

　　*说到RAM，如果你没有概念，先知道他可以以O（1）时间访问任意地址的元素即可，这很重要，直接说明了为何有些数据结构访问元素时间复杂度为O(1)

e.g：看下面递归的内存处理过程

def recSumFirstN(n):

　　if n == 0:

　　　　return 0

　　return recSumFirstN(n-1) + n

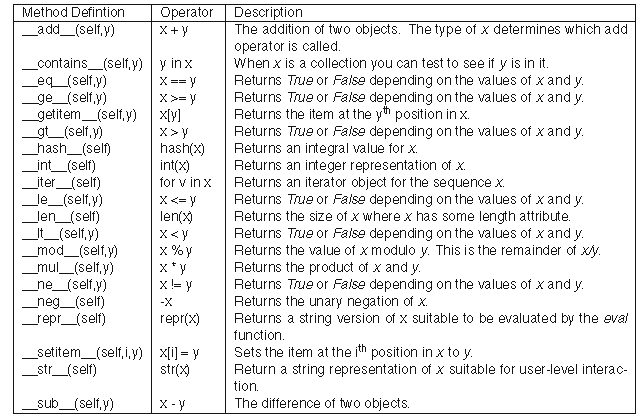
*六：运算符重载&类的内建方法

　　下表写明了一些常见的内建方法，在这里我讲了其中的一些