UVa 11768 格点判定（扩展欧几里得求线段整点）

https://vjudge.net/problem/UVA-11768

题意：

给定两个点A（x1，y1）和B（x2，y2），均为0.1的整数倍。统计选段AB穿过多少个整点。

思路：

做了这道题之后对于扩展欧几里得有了全面的了解。

根据两点式公式求出直线 ，那么ax+by=c 中的a、b、c都可以确定下来了。

接下来首先去计算出一组解(x0,y0)，因为根据这一组解，你可以写出它的任意解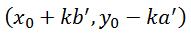，其中，K取任何整数。

需要注意的是，这个 a' 和 b' 是很重要的，比如说 b' ，它代表的是x每隔 b' ，就会出现一个整点。

所以这道题目的关键就是，我们先求出一组解，然后通过它的 b' 将x0改变成x，使得x在[x1,x2]区间之内，这样每 b' 个单位就有一个整点了，即

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 using namespace std;

 typedef long long LL;
 double X1,Y1,X2,Y2;

 void gcd(LL a,LL b,LL& d,LL& x,LL& y)
 {
     if(!b)  {d=a;x=;y=;}
     else { gcd(b,a%b,d,y,x); y-=x*(a/b);}
 }

 LL solve()
 {
     LL x1=X1*, y1=Y1*, x2=X2*, y2=Y2*;
     if(x1==x2)                    //平行y轴
     {
         if(x1%)  return ;      //原来的X1为小数,肯定不是整点
         if(Y2<Y1)  swap(Y1,Y2);
         return floor(Y2)-ceil(Y1)+;
     }
     if(y1==y2)
     {
         if(y1%)  return ;
         if(X2<X1)  swap(X1,X2);
         return  floor(X2)-ceil(X1)+;
     }
     LL a=(y2-y1)*, b=(x1-x2)*, c=y2*x1-y1*x2;  //c相当于扩大了100倍，所以前面还得乘10
     LL d,x,y;
     gcd(a,b,d,x,y);
     if(c%d)   return ;      //扩展欧几里得算法无解的判断

     x=x*c/d; y=y*c/d;        //获得一组整数解(x,y)
     b=abs(b/d);             //这里的b其实就是b'

     if(X1>X2)   swap(X1,X2);
     x1=ceil(X1);
     x2=floor(X2);
     if(x1>x2) return ;

     x=x+(x1-x)/b*b;        //使x进入[x1,x2]的区间内
     if(x<x1)  x+=b;
     if(x>x2)  return ;
     return (x2-x)/b+;
 }

 int main()
 {
     //freopen("D:\\input.txt","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%lf%lf%lf%lf",&X1,&Y1,&X2,&Y2);
         LL ans = solve();
         printf("%lld\n",ans);
     }
     return ;
 }