斜率优化dp学习

用了一堂半的课才彻底搞懂。其他神犇写的博客或多或少有点小bug，所以orzzz不才斗胆重新写一个。

里面大量穿用其他神犇的原话，就不逐一标明出处了。

引用资料 Accept的博客 MathonL的博客

首先是最经典的题的题面。

HDU 3507，很适合的一个入门题。

大概题意就是要输出$N$个数字$a[N]$，输出的时候可以连续连续的输出，每连续输出一串，它的费用是 “这串数字和的平方加上一个常数$M$”。

我们设$dp[i]$表示输出到$i$的时候最少的花费，$S[i]$表示从$a[1]$到$a[i-1]$的数字和。注意这里为了方便起见前缀和与一般的有区别。

则有：$dp[i]=min \left\{ dp[j]+(S[i+1]-S[j])^2+M \right\} (j<i)$

复杂度显然是$O(n^2)$的。对于$500000$的$n$显然过不了。那么我们想，能否在$O(1)$时间内找到所有转移里最优的那个呢？

我们假设在求解$dp[i]$时，存在$j,k(j>k)$使得从$j$转移比从$k$转移更优，那么需要满足条件：

$dp[j]+(S[i+1]-S[j])^2+M<dp[k]+(S[i+1]-S[k])^2+M$

展开上式

$dp[j]+S[i+1]^2-2S[i+1]S[j]+S[j]^2+M<dp[k]+S[i+1]^2-2S[i+1]S[k]+S[k]^2+M$

移项并消去再合并同类项得

$dp[j]-dp[k]+S[j]^2-S[k]^2<2S[i+1](S[j]-S[k])$

把$S[j]-S[k]$除过去，得到

$\frac{dp[j]-dp[k]+S[j]^2-S[k]^2}{S[j]-S[k]}<2S[i+1]$

我们设$f[x]=dp[x]+S[x]^2$，就化成了

$\frac{f[j]-f[k]}{S[j]-S[k]}<2S[i+1]$

即当$(j>k)$时，若$\frac{f[j]-f[k]}{S[j]-S[k]}<2S[i+1]$，则$j$对更新$dp[i]$比$k$更新$dp[i]$优。

休息一下qwq。这个东西好像斜率。

当一个数的$dp$值求完了，它的$f$值也跟着确定，我们就可以在空间中绘制出点$(S[i],f[i])$。这个点代表已经求出$dp$值的一个点。

当我们要求解$dp[t]$时，如果可用的集合里存在这样三个点，位置关系如图所示：

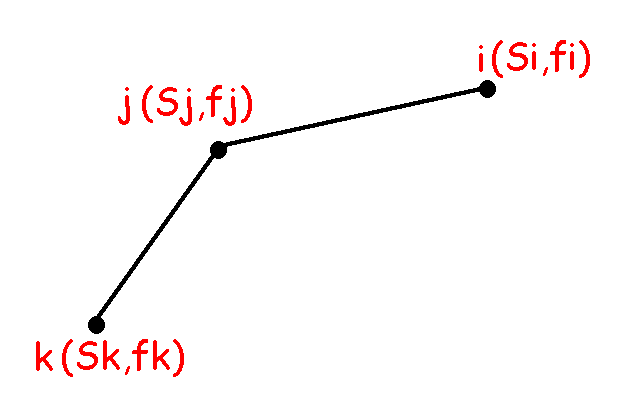
那么显然

$\frac{f[j]-f[k]}{S[j]-S[k]}>\frac{f[i]-f[j]}{S[i]-S[j]}$

这时候他们和$2S[t+1]$的关系有3种：

·$\frac{f[j]-f[k]}{S[j]-S[k]}>\frac{f[i]-f[j]}{S[i]-S[j]}>2S[t+1]$

那么$j$比$i$优，$k$比$j$优。

·$\frac{f[j]-f[k]}{S[j]-S[k]}>2S[t+1]>\frac{f[i]-f[j]}{S[i]-S[j]}$

那么$i$比$j$优，$k$比$j$优。

·$2S[t+1]>\frac{f[j]-f[k]}{S[j]-S[k]}>\frac{f[i]-f[j]}{S[i]-S[j]}$

那么$i$比$j$优，$j$比$k$优。

综上，不管什么样的$S[t+1]$，从$j$转移都不会是最佳方案。那么用一个数据结构维护一个凸包（下凸），每加入一个点就删去一些点，使其维持凸包的形态。最优转移一定在这个凸包中。

但还是不能$O(1)$对吧。在凸包里，谁又是最最优呢？

首先一定数据结构里的凸包一定会是这样的：

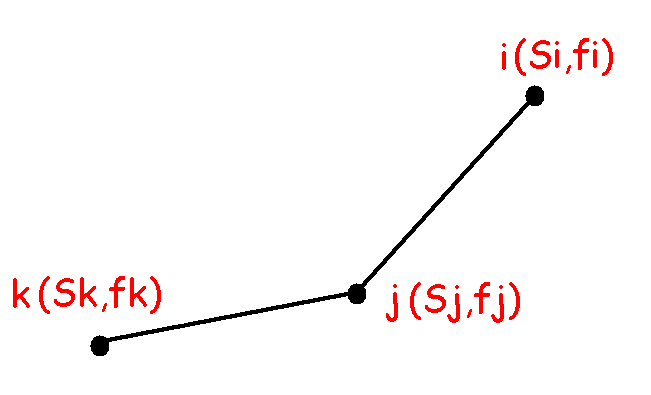
假设$\overrightarrow{ji}$的斜率$>2S[t+1]$且$\overrightarrow{kj}$的斜率$<2S[t+1]$从图形特点我们可以发现$j$点比所有比$k$小的点都优，比所有比$i$大的也优。所以对于我们二分查找斜率比$2S[t+1]$小的编号最大的点，就是最优的转移点。由于$S[i]$也满足单调性，我们还可以直接维护一个单调队列就能解决这个问题。

推广一下，如果不等式右侧不是像$S[i+1]$这样的单调函数，二分就好了。

所有小于等于的情况我都没提，想一想就知道了。重要的是思想啊对不对~

（我会说我一道斜率优化题都没做就写了这篇博客吗

---

upd1:

光会思想没有用啊，，，边界条件的处理很蛋疼的说

还是要自己写几遍qwq

upd2:

更正了一个bug，由@Duan2baka发现。不好好女装居然来看我这篇菜鸡博客。

upd3:

dp式子都写错了。。。感谢@自为风月马前卒指正

upd4:

我这bug也够多了哈。。感谢@belief01指正

upd5:

又改了一处不严谨的地方，感谢@ToRe

如果影响大家曾经的阅读深表歉意~虽然不是老师，但是千万不要误人子弟啊。。