kd树的原理

  kd树就是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构，可以运用在k近邻法中，实现快速k近邻搜索。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分。
   假设数据集\(T\)的大小是\(m*n\),即\(T={x_1,x_2,...x_m}\),其中\(x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T，i=1,2,...m\)。构建Kd树的过程大致如下。
  对所有的数据,以\(x^{(1)}\)为轴，即取\(x_i^{(1)}，i=1,2,...m\),并求得其中位数\(mid^{(1)}\)，\(mid^{(1)}\)对应的点即为根节点，以\(mid^{(1)}\)为切分点，将剩余数据分为两个集合，左子树对应小于切分点的区域，右子树对应大于切分点的区域，然后针对每个集合，以\(x^{(2)}\)为轴，重复上述过程，继续切分为两个集合，然后不断重复上述过程，依次选择\(x^{(j)}，j=1,2,...,n\)为轴，直到切分得到的集合中只有一个数据为止。
   kd树的构造相对简单，那么如何利用kd树进行搜索？
  给定一个目标点，搜索其最近邻，首先按照“左小右大”的规则，找到目标点所属区域对应的叶节点，然后从该叶节点出发，依次回退到父节点，不断查找与目标点最邻近的点，当确定不可能存在更近的节点时终止，这样搜索就被限制在空间的局部区域上，效率大大提高。
  具体来说，
  （1）从根节点出发，按照“左小右大”的规则，找到目标点所属区域对应的叶节点
  （2）然后从该叶节点出发，向上回退，在回退到的每个父节点\(f\)上，执行一下两种操作：
    (a)判断\(f\)与目标点的距离是否比当前最近距离更近，如果是，则将当前最近点更新为\(f\)
    (b)当前最近点一定存在于\(f\)的一个子结点对应的区域中，即一定存在于\(f\)对应的区域中，即有可能\(f\)另一个   子结点距离目标点更近。判断目标点是否距离\(f\)另一个子结点对应区域更近，具体地，判断目标点与\(f\)对应的切  分轴 的距离是否小于当前最小距离，如果小于，从该子结点出发，重复执行步骤（2）
  （3）当回退到根节点并完成对根节点步骤（2）中的两步操作时，搜索结束。当前最近点即为目标点的最近邻点。
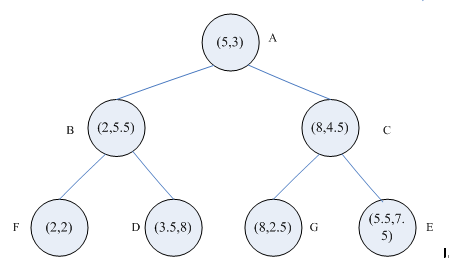
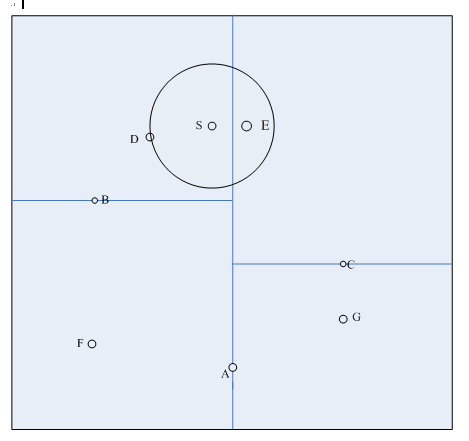
以一个具体例子说明。如图1是生成的一颗kd树，特征空间划分如图2所示，要求目标点S(4.5,7.5)的最近邻点。

  搜索过程如下：
  （1）首先在kd树中找到了包含目标点S的叶节点D，D即为当前最近点，两点之间的距离是当前最近距离dist；
  （2）向上回退到点B，点B距离点S更远，并且点B以\(x^{(2)}=5.5\)为切分轴，S距离\(x^{(2)}=5.5\)的距离大于dist，不用考虑点F；
  （3）继续向上回退到根节点点A，点A距离点S更远，但是点A以\(x^{(1)}=5\)为切分轴，S距离\(x^{(1)}=5\)的距离小于dist，那么点S有可能距离A的右子树区域C中的点更近
  （4）从点C出发，一直访问到点E，点E比点D距离点S更近，点E成为当前最近点，两点之间的距离是当前最近距离dist；
  （5）从点E向上回退到点C，点C距离点S更远，并且点C以\(x^{(2)}=4.5\)为切分轴，S距离\(x^{(2)}=4.5\)的距离大于dist，不用考虑点G
  （6）继续向上回退，再次回退到了根节点A，结束搜索，点E即为点S的最近邻点。