【原创】通俗易懂的讲解KMP算法(字符串匹配算法)及代码实现

一、本文简介

本文的目的是简单明了的讲解KMP算法的思想及实现过程。

网上的文章的确有些杂乱，有的过浅，有的太深，希望本文对初学者是非常友好的。

其实KMP算法有一些改良版，这些是在理解KMP核心思想后的优化。

所以本文重点是讲解KMP算法的核心，文章最后会有涉及一些改良过程。

二、KMP算法简介

KMP算法是字符串匹配算法的一种。它以三个发明者命名，Knuth-Morris-Pratt，起头的那个K就是著名科学家Donald Knuth。

三、KMP算法行走过程

首先我们先定义两个字符串作为示例，被匹配串 S = "abcabdabcabeab"，匹配串 T = "abcabeab"。

我们的目标就是确定S中是否包含T。

KMP算法的核心是分析匹配串 T 的特征，看看匹配串 T 能告诉我们什么信息。我把 T 着色，如下

T = "abcabeab"

现在看起来似乎比较明显了，三个着色点都是重复的 "ab"，似乎这个 T 能告诉我们它有重复的子串"ab"可以利用。那么它们到底怎么用？先不讲具体怎么用，先走一遍KMP这个过程，但是大家需要留意这个"ab"。

1.　　

我们发现T在匹配成功 "abcab" 后到"e"时和S子串的"d"匹配不成功了。

这个时候我们可以得到的先验就是目前T匹配过的S子串，就是"abcab"。而T本身就是"ab"重复的。所以"abcab"可以直接跳到第二个重复"ab"的位置，因为"abcab"中其它字符串开头不可能产生和T对应的匹配，这是很直观的。

因此T应该直接后移三个位置，并且用第三位的"c"和S刚才不匹配的"d"进行比较。

可以发现，S匹配的过程是不会回退的。因此匹配过程是S从头到尾的一遍扫描(中间可能因为匹配成功退出)，所以这个查找过程是O(N)的复杂度。

2.

此时的匹配串是 "ab"， 它告诉我们目前匹配的是"ab"。这个不像"abcab"出现了重复"ab"，所以我们知道包括S[5]的"d"之前的子串是垃圾串。因此跳过S[5]重新开始匹配T。

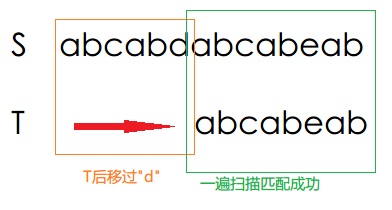
最后完成匹配，可见，这样一次对S的扫描完成了对T的查找。

那么对于机器如何实现？第四节会分析。

四、KMP算法核心解析

对于上面的过程，我们抽离出来的话，问题的根本就是对T串重复情况的一个判定。不管S是什么串，只要对T的构造模式分析清楚就可以完成上述跳转过程。

因此需要一个数组记录这个T的 模式函数。

这里先给出这个T的模式函数

1.每个字母对应模式函数的值就是匹配到当前位置 i 后，下一次T开始进行比较的下标。

2.而S的移动长度为 i - F(i-1)。

对应上面两个问题

1.比如上面的匹配到的 "abcab" ，是T匹配到 T[5] 即"e"的时候出错的。那么我们需要查看上一个字符的模式函数值，因为上一个函数值才代表了已经匹配的串。

发现F(4)=2，说明下次比较从T[2]即"c"开始。因为"abcab"有重复"ab"，第一个"ab"不需要比较。

2.而S下标移动多少呢？S下标的移动即找到T的初试位置对应的S的下标。对应上面第二张图，S[3]和T的移动对应起来了。3的获得就是通过上面公式 5-F(4)得到的。其实这个结果和1得到匹配位置的思路是一样的，不过又向前移动对齐了开头。

为什么如此构造这个模式函数？

就是因为F值表示了对于位置 i， T[i]有无重复，并且重复下标的位置在哪(F[i])。既然我们获取了重复下标的位置，那么其它的相关值可以推出来了。

基于这个思路，再给出另外两个T串的模式函数值，帮助大家思考。

1.

2.

如何快速构造这个模式函数？

这个留给大家思考一下了，应该也比较直接了，注意是查找重复位置。如果不大明白，可以参考下面的代码。

五、KMP算法实现

再添加个例子帮助大家思考：

S1 = "aaaaaaaaaaaaaaaab"  S2 = "aaaaafaaaaaaaaab"   T = "aaaab"

对于S1和S2两种情况，应如何匹配。

代码如下：

 1 /*
 2     return val means the begin pos of haystack
 3     -1 means no matching substring
 4 */
 5 int KMP(char *haystack, char *needle) {
 6     // pre-process
 7     if(haystack[0] == 0 && needle[0] == 0)
 8         return 0;
 9
10     int i, j, k, min, cur;
11
12     //construct F(t) in vector len
13     vector<int > len;
14     len.push_back(0);
15     for(i=1; needle[i] != 0; i++){
16         if(len[i-1] == 0){
17             if(needle[i] == needle[0])
18                 len.push_back(1);
19             else
20                 len.push_back(0);
21         }else{
22             if(needle[i] == needle[len[i-1]])
23                 len.push_back(len[i-1]+1);
24             else
25                 len.push_back(0);
26         }
27     }
28     // KMP finder
29     j = 0;
30     for(i=0; haystack[i] != 0; ) {
31         // matching
32         for(; needle[j] != 0; j++) {
33             if(haystack[i+j] != needle[j])
34                 break;
35         }
36         //finded
37         if(needle[j] == 0)
38             return i;
39         else{ // jump
40             if(j){
41                 cur = j - len[j-1];
42                 i += cur;
43                 j = len[j-1];
44             }else{
45                 j = 0;
46                 i++;
47             }
48         }
49     }
50     //match failed
51     return -1;
52 }

六、KMP算法改进

KMP算法有一些改进版本加速查找，一般可以通过S串中的一些信息加速匹配过程。

比如若  S = "aaaaaaaafaaaaaaaaaaaab", T = "aaaaaaab"。

在查找过程中，S中间的 "f" 起到了阻挡作用。但是由于我们只是考虑T的先验信息，遇到"f" 不匹配会导致T每次后移一步进行新的匹配，直到T的开头碰到了"f"。

但是如果我们加入"f"这个原串S的信息，由于"f" ！= "b" && "f" != "a" && i-1 = F(i-1) ，所以直接跳到"f"后进行新的匹配会更快速的查找。

但是这些改进都是基于KMP基础算法之上的，因此把握核心要点不仅省时省力，更能有效扩展。

七、参考

[1] 《字符串匹配的KMP算法》 http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

[2] 算法导论

转载请注明出处~   http://www.cnblogs.com/xiaoboCSer/p/4237941.html