HDU 2147kiki's game（巴什博弈变形）

题目链接

思路如下

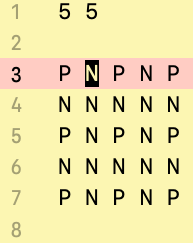
P ： 必胜点，那个人先走到 含P的点，那个这个人一定会输，

N：必败点，谁走到这个点谁输！

在这一个题中： 某个点是P还是 N，之与 ⬅️左边第一个点、⬇️下边第一个点、↙️左下第一个点有关,只要这个三个点中 只要有一个是 P ，那么我们 要求的这个点就是P ，否则才是N。

剩下的就是找规律：对于这一个题 如果 m、n 都是奇数的话：那么小明从

右上角（1，m）出发，所能到达三个 点全是 N小明必败，否则小明一定赢

题解如下

#include<iostream>
#include<algorithm>
using namespace std;

const int Len  = 1e5 + 5;
int ar[Len];
int m,n;

bool group(int mid)
{
    int sum = 0;
    int cnt = 1;
    for(int i = 0; i < m; i ++)
    {
        if(sum + ar[i] <= mid)
        {
            sum += ar[i];
        }
        else
        {
            sum = ar[i];
            cnt ++;
        }
    }
    if(cnt > n)
        return true;
    else
        return false;
}

void Binary_search(int l,int r)
{
    int mid;
    while(l <= r)
    {
        mid = (l + r) / 2;
        if(group(mid))
        {
            l = mid + 1;
        }
        else
        {
            r = mid - 1;
        }
    }
    printf("%d",mid);
}

int main()
{
    //freopen("A.txt","r",stdin);
    scanf("%d %d",&m,&n);
    int sum = 0;
    int mx = -1;
    for(int i = 0; i < m; i ++)
    {
        scanf("%d",&ar[i]);
        sum += ar[i];
        mx = max(mx , ar[i]);
    }
    Binary_search(mx,sum);

    return 0;
}