P5676 [GZOI2017]小z玩游戏【Tarjan】

小z玩游戏

Tarjan算是板子题吧，但是要稍微做一些修改，建边需要多考虑，建立“虚点”。

题目描述

小 z 很无聊。

小 z 要玩游戏。

小 z 有\(N\)个新游戏，第\(i\)个游戏看上去的有趣程度为\(w_i\)。小 z 很挑，他只会玩看上去的有趣程度是自己兴奋程度整数倍的游戏。由于游戏实际上有好玩的也有不好玩的，玩完第\(i\)个游戏后，小 z 的兴奋程度会变为\(e_i\) 。

已知小 z 初始兴奋程度为\(1\)，请问小 z 有多少个游戏可能会玩两次？

输入格式

第一行一个正整数\(T\)，表示测试数据组数，最多\(10\)组。

对于每组测试数据：

第一行一个正整数\(N\)，表示游戏的个数。第二行\(N\)个正整数，第\(i\)个数\(w_i\) ，表示第\(i\)个游戏看上去的有趣程度为\(w_i\) 。第三行\(N\)个正整数，第\(i\)个数\(e_i\)​，表示小 z 玩完第\(i\)个游戏后，小 z 的兴奋程度会变为\(e_i\) 。

输出格式

共\(T\)行。

每行一个正整数，表示对应测试数据，小 z 可能会玩两次的游戏数量。

输入输出样例

输入

5

1

100000

100000

5

1 2 6 15 35

5 7 9 2 3

5

2 3 5 35 21

7 11 7 3 2

10

6 15 77 12 24 37 35 99 55 42

4 2 5 7 11 3 6 8 9 10

10

6540 5604 567 57065 60 670 6870 1230 465 6540

12 5 37 3 34 13 17 18 10 12

输出

1

3

3

8

5

说明/提示

【样例第 2 组数据解释】

数字代表游戏编号，箭头表示下一个。

可能的情况 \(1：2->5->4->2\)

可能的情况 \(2：5->4->2->5\)

可能的情况 \(3：4->2->5->4\)

所以小 z 可能玩 \(2,4,5\) 两次。

小 z 无论如何都不能玩 \(1\) 或 \(3\) 两次。

【数据约束】

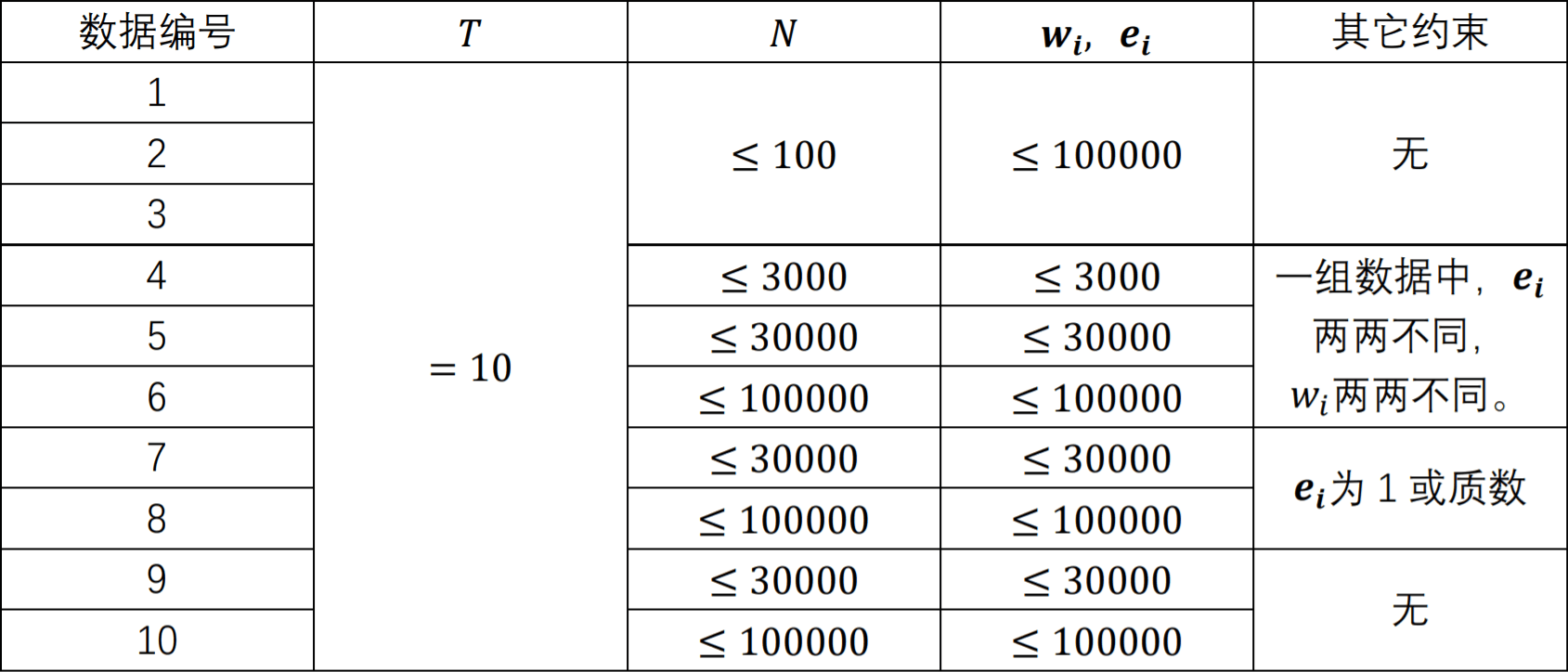
分析

这个题看完题目，就很容易能够想到如果一个游戏能玩两边，那么肯定是游戏与游戏之间玩的时候形成了一个环，那么久可以想到用\(Tarjan\)求强连通分量，然后找出每个环的大小，最后加和就可以。但是如果把每一个游戏和玩完游戏的兴奋程度都建边，看一下数据范围，肯定是不能\(AC\)的，所以我们要考虑一下怎么建边。因为每玩一个游戏，兴奋程度都会有变化，而只有游戏的兴奋程度是他的兴奋程度的整数倍才会去玩，所以我们从第几个游戏到玩完这个游戏的兴奋程度建边，然后在每个游戏的有趣程度和此游戏中再建一条边，最后再从每个兴奋程度到它所能满足的有趣程度建一个边，这样就实现了原来\(n^2\)的建图方式来达到从当前游戏对下一个能玩的游戏建边的目的。下边是第二组样例中建好的图



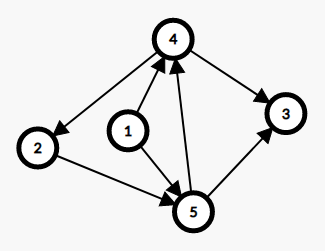
这个图中强连通分量一共有三个点，所以答案就是三，然后按照优化的建边方法，就可以\(AC\)了（温馨提示：\(Tarjan\)一定要认真写，本人\(Tarjan\)写挂了，乱七八糟，重写一遍才改过来。）

在\(Tarjan\) 的时候，要记录强连通分量大小，大于1就标记当前点，然后运行的时候在强连通分量里的也要都标记，最后从\(1\)到\(n\)统计标记数，得出答案。

时间复杂度的证明，借用一下\(Luogu\)大佬的分析

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e6+10;
int head[maxn],vis[maxn];
int c[maxn];
int num;
int dfn[maxn],low[maxn];
int next[maxn],ver[maxn];
int tot,cnt;
int sta[maxn];
int top;
void Add(int x,int y){//建图
	ver[++tot] = y;
	next[tot] = head[x];
	head[x] = tot;
}
void Tarjan(int u){//求值
	sta[++top]=u;
	dfn[u]=low[u]=++num;
	for(int i=head[u];i;i=next[i]){
		int v=ver[i];
		if(!dfn[v]){
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}else if(!c[v])
		low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u]){
		c[u]=++cnt;
		int siz=1;
		while(sta[top]!=u){
			c[sta[top]]=cnt;//标记当前点在第几个分量里
			vis[sta[top]]=1;//标记当前点
			siz++;//枚举一个点的时候就大小加一
			top--;
		}
		if(siz>1)vis[u]=1;//不是一个点的强连通分量就标记当前点
		--top;
	}
}
int n;
int T;
int main(){
	scanf("%d",&T);
	while(T--){//初始化
		memset(vis,0,sizeof(vis));
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(c,0,sizeof(c));
		memset(next,0,sizeof(next));
		memset(ver,0,sizeof(ver));
		memset(sta,0,sizeof(sta));
		memset(head,0,sizeof(head));
		num = 0;
		tot = 0;
		cnt = 0;
		top = 0;
		scanf("%d",&n);
		int Max = 0;
		for(int i=1,x;i<=n;++i){//从玩完这个游戏的兴奋度到这个游戏建边
			scanf("%d",&x);
			Add(n+x,i);
			Max = max(Max,x);
		}
		for(int i=1,x;i<=n;++i){//从该游戏到该游戏的有趣度建边
			scanf("%d",&x);
			Add(i,n+x);
		}
		for(int i=1;i<=Max;++i){//从该游戏兴奋度到有趣度建边，相当于连接上能连续玩的两个点
			for(int j=2;j*i<=Max;++j){
				Add(n+i,n+i*j);
			}
		}
		for(int i=1;i<=n;++i){
			if(!dfn[i])Tarjan(i);
		}
		int ans = 0;
		for(int i=1;i<=n;++i){//统计答案
			if(vis[i])ans++;
		}
		printf("%d\n",ans);
	}
}