最短路径——Dijkstar算法

背景：本文是在小甲鱼数据结构教学视频中的代码的基础上，添加详细注释而完成的。该段代码并不完整，仅摘录了核心算法部分，结合自己的思考，谈谈理解。

Dijkstar算法理解：

Dijkstar算法的核心思想就是通过一次一次的迭代，逐个寻找起始顶点到图中每一个顶点的最短路径，并在确定一个顶点的最短路径之后，设置标志位，同时根据最新确定的顶点的最短路径，对其他与之相关顶点的最短路径进行修正和更新。

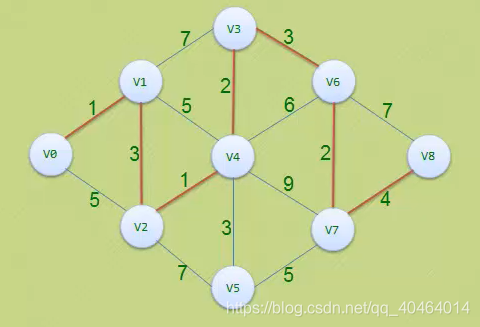
如图（摘录自小甲鱼教学视频中的图片），是一个带有权值的连通网：

根据上图可以列写出该连通网的邻接矩阵，为了方便直观的理解：

权值	V0	V1	V2	V3	V4	V5	V6	V7	V8
V0	0	1	5	Ꚙ	Ꚙ	Ꚙ	Ꚙ	Ꚙ	Ꚙ
V1	1	0	3	7	5	Ꚙ	Ꚙ	Ꚙ	Ꚙ
V2	5	3	0	Ꚙ	1	7	Ꚙ	Ꚙ	Ꚙ
V3	Ꚙ	7	Ꚙ	0	2	Ꚙ	3	Ꚙ	Ꚙ
V4	Ꚙ	5	1	2	0	3	6	9	Ꚙ
V5	Ꚙ	Ꚙ	7	Ꚙ	3	0	Ꚙ	5	Ꚙ
V6	Ꚙ	Ꚙ	Ꚙ	3	6	Ꚙ	0	2	7
V7	Ꚙ	Ꚙ	Ꚙ	Ꚙ	9	5	2	0	4
V8	Ꚙ	Ꚙ	Ꚙ	Ꚙ	Ꚙ	Ꚙ	7	4	0

算法流程：（叙述过程中用D数组表示各点最短路径的权值和数组，用P数组表示最短路径的下标数组）

算法流程和最下方的算法代码结合在一起看，方便理解。

1、第一个循环

D数组初始化时幅值为邻接矩阵中V0（起始顶点）行。V0顶点默认已经确定了最短路径。

第一个for循环，首先在未确定最短路径的所有顶点中寻找与V0直接相连，且权值最小的顶点，得到k = 1（k保存前驱顶点）；min = 1（min保存到达前驱顶点的最短路径权值和），在这个for循环中，找到的这个顶点可以直接确定找到了最短路径（因为每次在第二个for循环中，都进行了对于其他未确定最短路径的顶点的路径优化）。

第二个for循环对于路径进行优化，优化原则为：如果 【到达前驱顶点的权值和（即min）+ 前驱顶点到达其他未确定最短路径的顶点的权值 < 当前D数组中达到该顶点的权值和 】则说明当前到达该顶点的路径不够优化，此时即可采用经过当前前驱顶点到达那个顶点的路径替换之前的路径，即同时更新P数组，将当前的k中保存的前驱顶点作为那个顶点的前驱。

D数组	V0	V1	V2	V3	V4	V5	V6	V7	V8
k=1,min=1	0	1	5	Ꚙ	Ꚙ	Ꚙ	Ꚙ	Ꚙ	Ꚙ
优化路径	0	1	4	8	6	Ꚙ	Ꚙ	Ꚙ	Ꚙ

P数组	V0	V1	V2	V3	V4	V5	V6	V7	V8
k=1 优化	0	0	1	1	1	0	0	0	0

2、第二个循环

相同的原理进行一次迭代，结果如下（注意自己过流程的时候，对照上面的邻接矩阵）：

D数组	V0	V1	V2	V3	V4	V5	V6	V7	V8
k=2,min=4	0	1	4	8	6	Ꚙ	Ꚙ	Ꚙ	Ꚙ
优化路径	0	1	4	8	5	11	Ꚙ	Ꚙ	Ꚙ

P数组	V0	V1	V2	V3	V4	V5	V6	V7	V8
k=2 优化	0	0	1	1	2	2	0	0	0

3、第三个循环

相同的原理进行一次迭代，结果如下：

D数组	V0	V1	V2	V3	V4	V5	V6	V7	V8
k=4,min=5	0	1	4	8	5	11	Ꚙ	Ꚙ	Ꚙ
优化路径	0	1	4	7	5	8	11	14	Ꚙ

P数组	V0	V1	V2	V3	V4	V5	V6	V7	V8
k=4 优化	0	0	1	4	2	4	4	4	0

......如此循环n次（n为顶点数），即可已得到最短路径，结果如下：

结果	V0	V1	V2	V3	V4	V5	V6	V7	V8
D数组	0	1	4	7	5	8	10	12	16
P数组	0	0	1	4	2	4	3	6	7
final数组	1	1	1	1	1	1	1	1	1

根据D数组可以得到从起始点到达任何一个顶点的最短路径权值和，根据P数组可以得到每一个顶点的最短路径中的前驱顶点，进而可以连接生成最短路径，该例题中到达V8的最短路径为：

代码如下：

#define MAXVEX 	9
#define INFINITY 	65535

/* 用来存储最短路径下标的数组 */
typedef int Patharc[MAXVEX];
/* 用来存储到各点最短路径的权值和 */
typedef int ShortPathTable[MAXVEX];

void ShortestPath_Dijkstar(MGragh G,int V0,Patharc *P,ShortPathTable *D)
{
	int v,w,k,min;
	/* final[w] = 1表示已经求得顶点Vo到Vw的最短路径 */
	int final[MAXVEX];

	/* init */
	for(v=0;v<G.numVertexes;v++)
	{
		/* 全部顶点初始化为未找到最短路径 */
		final[v] = 0;
		/* 起始点V0到其他点之间的最短路径数组赋初始值:即邻接矩阵中V0行的值 */
		/* 即到与V0有有直接连线的点的最短路径为边的权值;无直接连线的点的最短路径为最大值 */
		(*D)[v] = G.arc[V0][v];
		/* 初始化路径数组P为0 */
		(*P)[v] = 0;
	}
	/* V0到V0的路径为0 */
	(*D)[V0] = 0;
	/* V0到V0不需要求路径 */
	final[V0] = 1;

	/* 主循环 每次求得V0到某个V顶点的最短路径 */
	/* 从v=1开始循环因为v0点的最短路径已经自动赋值为0 */
	for(v=1;v<G.numVertexes;v++)
	{
		min = INFINITY;
        /* 第一个for循环 */
		for(w=0;w<G.numVertexes;w++)
		{
			/* 判断final数组(即未求得最短路径) */
			/* 仅对未确定最短路径的顶点 在D数组中寻找最小权值 */
			/* 因为经过下一个for循环的最短路径修正之后，未确定最短路径的顶点中到V0权值最小的顶点，经过的必然是到该店的最短路径 */
			if(!final[w] && (*D)[w]<min)
			{
				/* k暂时保存前驱顶点 */
				k = w;
				/* min暂时保存到达前驱顶点的最短路径权值和 */
				min = (*D)[w];
			}
		}
		/* 标志当前顶点以找到了最短路径 */
		final[k] = 1;

		/* 在找到拥有最短路径的最新的一个顶点后，修正最短路径及距离 */
		/* 原先可能某些未确定最短路径的顶点，选择的路径不够优化(以此顶点的最优路径对其进行优化) */
        /* 第二个for循环 */
		for(w=0;w<G.numVertexes;w++)
		{
			/* 前驱顶点已经确认为最短路径(即min) */
			/* 如果经过之前保存的前驱顶点的路径比现在这条路径(D数组中原本的)的长度短的话 更新更优的路径 */
			if(!final[w] && (min+G.arc[k][w]<(*D)[w]))
			{
				/* 修改当前路径长度 */
				(*D)[w] = min+G.arc[k][w];
				/* 存放前驱顶点 */
				/* P数组存放前驱顶点 完成后即可通过P数组得到最短路径 */
				(*P)[w] = k;
			}
		}
	}
}

——cloud over sky

——2020/3/12