吴恩达深度学习第1课第4周-任意层人工神经网络(Artificial Neural Network，即ANN)（向量化）手写推导过程（我觉得已经很详细了）

学习了吴恩达老师深度学习工程师第一门课，受益匪浅，尤其是吴老师所用的符号系统，准确且易区分．

遵循吴老师的符号系统，我对任意层神经网络模型进行了详细的推导，形成笔记．

有人说推导任意层MLP很容易，我表示怀疑啊．难道又是我智商的问题嘛╮（╯＿╰）╭．

推导神经网络， 我用了一天．最后完成了，我就放心了，可以进行下一部分学习了：）

推这玩意是个脏活累活，直接记住向量化表示(结果)也是极好的.

顺便说一下，本文的图片若看不清，可以另存为本地文件放大看(scan的时候我定了较高的精度)，更清楚^^

该笔记目的为：记录推导过程，供自己复习．

0. 为推导顺利而总结的经验

该部分内容是我推导后才总结的．但我觉得应该放在最前面，最显眼的位置，里面的内容还是很重要的．

1. 搭建实例，明确符号系统，理顺正向、反向传播过程，明确 loss function

需要说明的是，loss function, dAL和任务有关．

我们模型输出层就１个单元，且为sigmoid单元. (原因是假定模型要跑一个二分类任务)

其他层用什么单元就无所谓了（我们的符号系统都能表示，如\(A^{[l]}=g^{[l]}(Z^{[l]})\)里面的\(g^{[l]}(\cdot)\)表示的就是模型中第\(l\)层所用的 activation function），如 sigmoid, relu, tanh单元或其他改进的relu单元．这些东西在吴老师的课程中都有详细讲解．

2. 考察dAL

3. 与大牛不符之dAL中的\(\frac{1}{m}\)为啥消失了？

dAL中的\(\frac{1}{m}\)为啥消失了？吴老师的推导中是没有\(\frac{1}{m}\)的，而我的推导里是有的．和超级大牛的答案不符，那就是我错了？（我错的地方请指出，谢谢啦）

**这个问题解决了，我的推导是对的！原因是：2017.11.13这天，我正在做吴恩达深度学习工程师第二课第一周编程作业，发现Ng老师提供的init_utils.py文件里的 backward_propagation(X, Y, cache)函数（关于一个三隐层神经网络的反向传播函数）中有这样一句话：dz3 = 1./m * (a3 - Y)，因此，我的推导是正确的，dAL应该有\(\frac{1}{m}\)这一项.

另外，根据链式法则，dAL若有1/m，那么后续的 dZ, dW, db就都不需要加1/m了．Andrew Ng 老师第一门课中，虽然 dAL 没有加 1/m，但后续的 dW, db都分别加了 1/m, 结果也是对的．

** init_utils.py的函数 backward_propagation(X, Y, cache)的完整代码如下：

def backward_propagation(X, Y, cache):
    """
    Implement the backward propagation presented in figure 2.

    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
    cache -- cache output from forward_propagation()

    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    m = X.shape[1]
    (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3) = cache

    dz3 = 1./m * (a3 - Y)  # <----------- 就是这句话，表明我的推导是正确的．
    dW3 = np.dot(dz3, a2.T)
    db3 = np.sum(dz3, axis=1, keepdims = True)

    da2 = np.dot(W3.T, dz3)
    dz2 = np.multiply(da2, np.int64(a2 > 0))
    dW2 = np.dot(dz2, a1.T)
    db2 = np.sum(dz2, axis=1, keepdims = True)

    da1 = np.dot(W2.T, dz2)
    dz1 = np.multiply(da1, np.int64(a1 > 0))
    dW1 = np.dot(dz1, X.T)
    db1 = np.sum(dz1, axis=1, keepdims = True)

    gradients = {"dz3": dz3, "dW3": dW3, "db3": db3,
                 "da2": da2, "dz2": dz2, "dW2": dW2, "db2": db2,
                 "da1": da1, "dz1": dz1, "dW1": dW1, "db1": db1}

    return gradients

我的推导：

4. 假定吴老师正确推导了dAL的前提下，推导dZL

5. \(dZ^{[l]}\)推\(dW^{[l]}\)(上)

推导dW以及后续参数时，我只管每一步有意义(仔细看笔记，您就能明白我的意思)，并能编程实现(虽然不是向量化的). 但最后推导的结果是可以向量化表示的(就能向量化编程喽)！

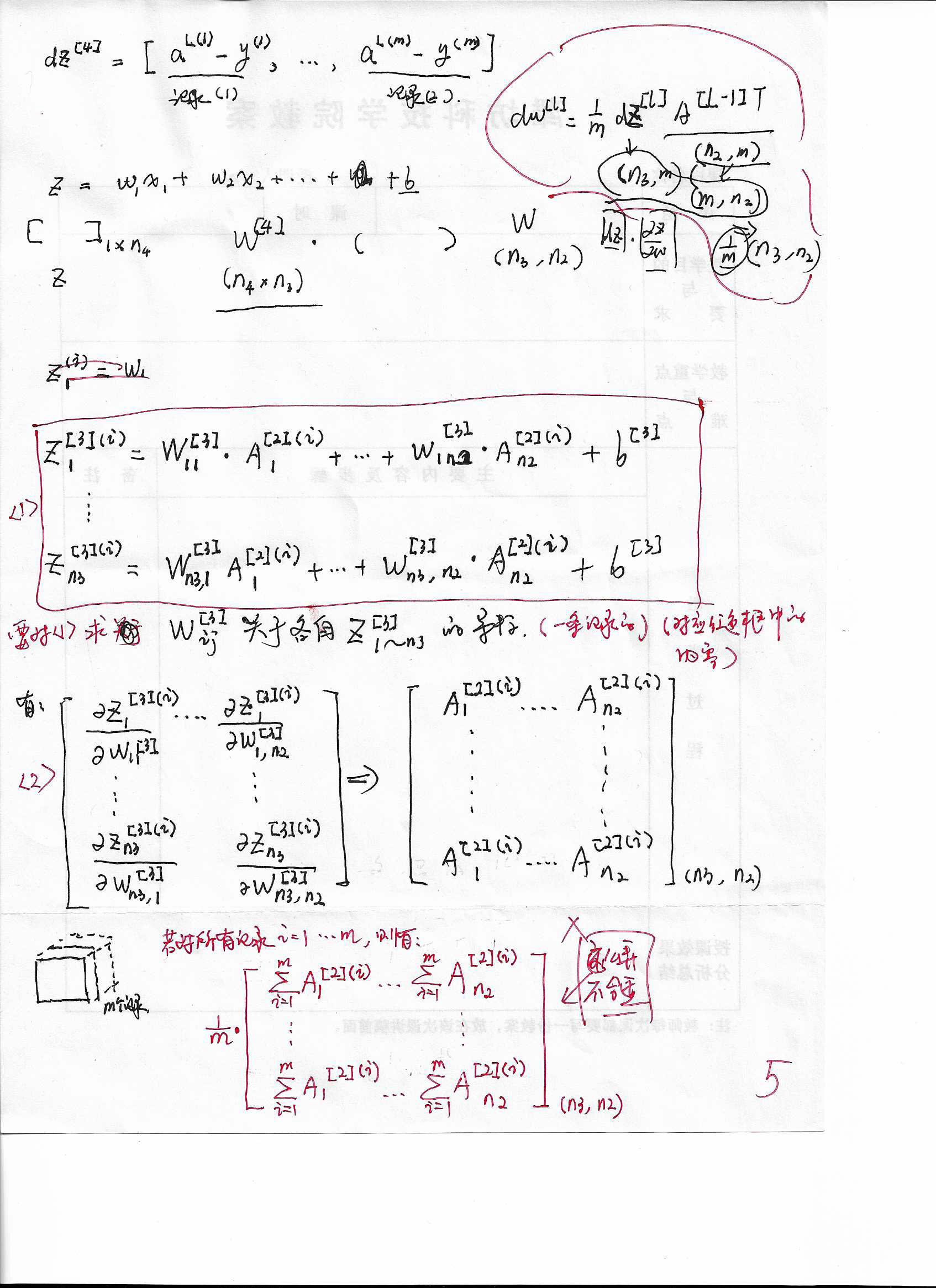
6. \(dZ^{[l]}\)推\(dW^{[l]}\)(中)

7. \(dZ^{[l]}\)推\(dW^{[l]}\)(下)

8. \(dZ^{[l]}\)推\(db^{[l]}\)

9. \(dZ^{[l]}\)推\(dA^{[l-1]}\)(上)

10. \(dZ^{[l]}\)推\(dA^{[l-1]}\)(下)

11. \(dA^{[l]}\)推\(dZ^{[l]}\)