RB-Tree删除详解

红黑树的删除操作较于插入操作，情况更为复杂：

考虑到红黑节点的差异性，我们在此通过红黑节点来考虑这个问题，即仅仅通过要删除的节点是红节点，还是黑节点来讨论不同的情况：

1  删除的红节点为叶子结点（此处为不考虑空叶子结点的模型）

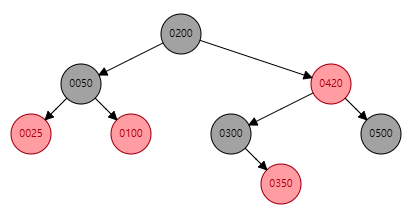
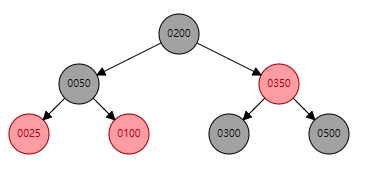
假如上图所示节点，需要删除：25，或者 350 ，我们来看看结果：

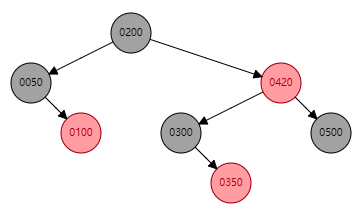
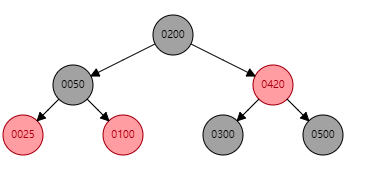
上图结果表明：如果待删除的红色节点为叶子结点（再次说明这里仅仅是不考虑空叶子节点的模型），则直接进行删除即可。

2  删除的红色节点不是叶子节点，如图中的420.  我们分析一下：如果删除的红色节点不是叶子节点，那么根据红黑树的性质，待删除节点的两个儿子节点均为黑色节点，而且它的父亲节点也为黑色节点。如果我们要 删除的节点是420。

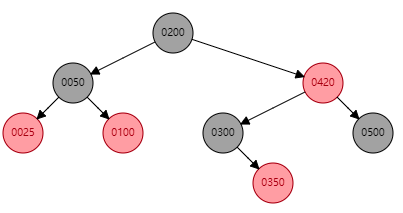
删除节点420之后，变为：

可见，如果删除非叶子节点的红色节点，该节点的值由其前驱节点代替，即其左子树的最右端的节点代替。如果替代后，树的平衡性没有被破坏，则该节点为红色。如果树的平衡性遭到破坏，需要对树的结构进行调整