二叉搜索树的平衡--AVL树和树的旋转

二叉搜索树只有保持平衡时其查找效率才会高。

要保持二叉搜索树的平衡不是一件易事。不过还是有一些非常经典的办法可以做到，其中最好的方法就是将二叉搜索树实现为AVL树。

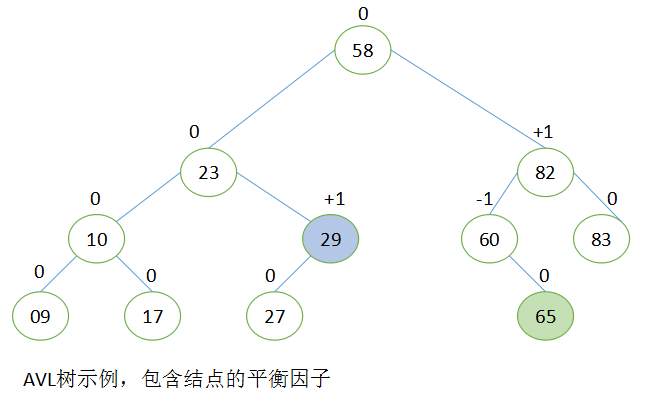
AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis，他们在 1962 年的论文 "An algorithm for the organization of information" 中发表了它。AVL树是一种特殊类型的二叉树，它的每个结点都保存一份额外的信息：结点的平衡因子。

结点的平衡因子 = 左子树的高度 - 右子树的高度

插入和删除操作都会导致AVL树的自我调整（自我平衡），使得所有结点的平衡因子保持为+1、-1或0。

当子树的根结点的平衡因子为+1时，它是左倾斜的（left-heavy)。

当子树的根结点的平衡因子为 -1时，它是右倾斜的(right-heavy)。

一颗子树的根结点的平衡因子就代表该子树的平衡性。

保持所有子树几乎都处于平衡状态，AVL树在总体上就能够基本保持平衡。

AVL树的基本查找、插入结点的操作和二叉树的操作一样。但是，当向AVL树中插入一个结点后，还有一些额外的工作要做。首先，必须计算因插入操作对平衡因子带来的改变。其次，如果任何平衡因子变成了+/-2，就必须从这个结点开始往下重新平衡这颗树，这个重新平衡的过程就称为旋转。

AVL树的旋转

旋转操作用来重新平衡树的某个部分。通过重新安排结点，使结点之间的关系始终保持左子结点小于父结点，父结点小于右子结点。使得该树仍然是一颗二叉搜索树。旋转过后，旋转子树中的所有结点的平衡因子都为+1、-1或0。

AVL树的旋转类型有4种，分别是LL(left-left)旋转、LR(left-right)旋转、RR(right-right)旋转和RL(right-left)旋转。

为方便理解在何时执行哪一种旋转，设x代表刚插入AVL树中的结点，设A为离x最近且平衡因子更改为2的绝对值的祖先。可以归纳为下面4种处理情况：

LL旋转

如下图所示，当x位于A的左子树的左子树上时，执行LL旋转。

设left为A的左子树，要执行LL旋转，将A的左指针指向left的右子结点，left的右指针指向A，将原来指向A的指针指向left。

旋转过后，将A和left的平衡因子都改为0。所有其他结点的平衡因子没有发生变化。

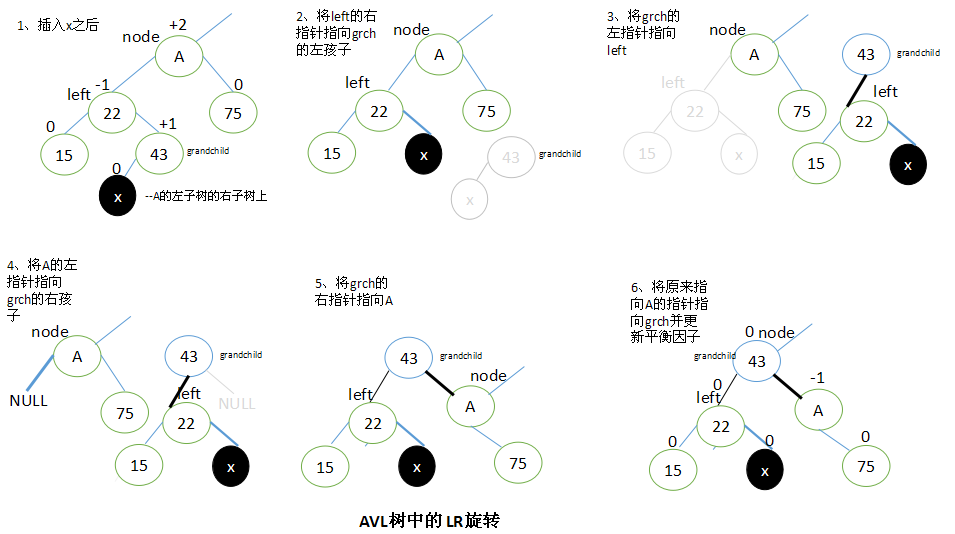
LR旋转

当x位于A的左子树的右子树上时，执行LR旋转。

设left是A的左子结点，并设A的子孙结点grandchild为left的右子结点。

要执行LR旋转，将left的右子结点指向grandchild的左子结点，grandchild的左子结点指向left，A的左子结点指向grandchild的右子结点，再将grandchild的右子结点指向A，最后将原来指向A的指针指向grandchild。

执行LR旋转之后，调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子值。

如果grandchild结点的原始平衡因子为+1，就将A的平衡因子设为-1，将left的平衡因子设为0。

如果grandchild结点的原始平衡因子为0，就将A和left的平衡因子都设置为0。

如果grandchild结点的原始平衡因子为-1，就将A的平衡因子设置为0，将left的平衡因子设置为+1。

在所有的情况下，grandchild的新平衡因子都是0。所有其他结点的平衡因子都没有改变。

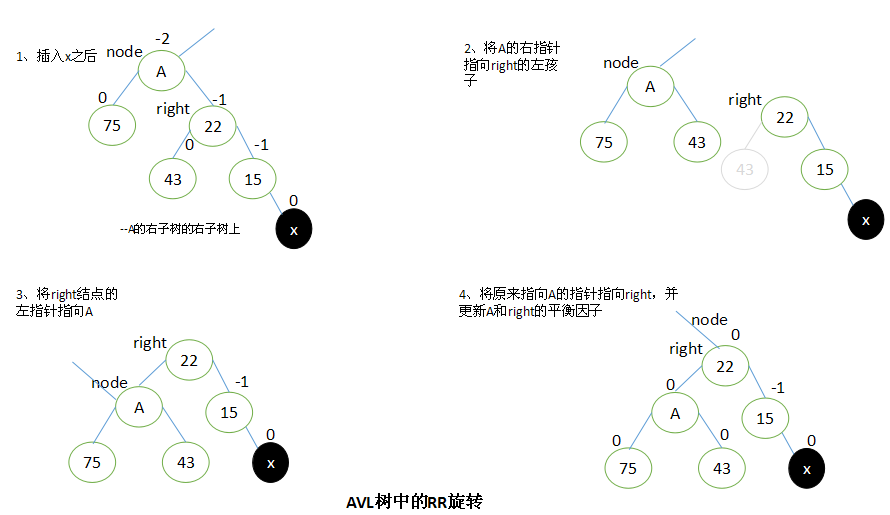
RR旋转

当x位于A的左子树的右子树上时，执行RR旋转。

RR旋转与LL旋转是对称的关系。

设A的右子结点为Right。要执行RR旋转，将A的右指针指向right的左子结点，right的左指针指向A，原来指向A的指针修改为指向right。

完成旋转以后，将A和left的平衡因子都修改为0。所有其他结点的平衡因子都没有改变。

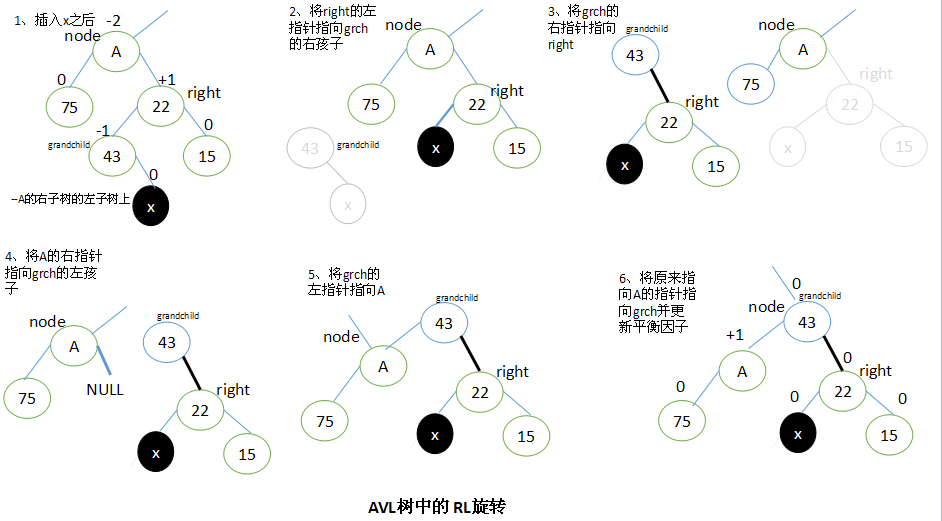
RL旋转

当x位于A的右子树的左子树上时，执行RL旋转。

RL旋转与LR旋转是对称的关系。

设A的右子结点为right，right的左子结点为grandchild。要执行RL旋转，将right结点的左子结点指向grandchild的右子结点，将grandchild的右子结点指向right，将A的右子结点指向grandchild的左子结点，将grandchild的左子结点指向A，最后将原来指向A的指针指向grandchild。

执行RL旋转以后，调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子。这里也有三种情况需要考虑：

如果grandchild的原始平衡因子值为+1，将A的平衡因子更新为0，right的更新为-1；

如果grandchild的原始平衡因子值为 0，将A和right的平衡因子都更新为0；

如果grandchild的原始平衡因子值为-1，将A的平衡因子更新为+1，right的更新为0；

在所有情况中，都将grandchild的新平衡因子设置为0。所有其他结点的平衡因子不发生改变。

来源：https://www.cnblogs.com/idreamo/p/8308336.html