简单的基于矩阵分解的推荐算法-PMF, NMF

介绍：

推荐系统中最为主流与经典的技术之一是协同过滤技术（Collaborative Filtering），它是基于这样的假设：用户如果在过去对某些项目产生过兴趣，那么将来他很可能依然对其保持热忱。其中协同过滤技术又可根据是否采用了机器学习思想建模的不同划分为基于内存的协同过滤（Memory-based CF）与基于模型的协同过滤技术（Model-based CF）。其中基于模型的协同过滤技术中尤为矩阵分解（Matrix Factorization）技术最为普遍和流行，因为它的可扩展性极好并且易于实现，因此接下来我们将梳理下推荐系统中出现过的经典的矩阵分解方法。

矩阵分解：

首先对于推荐系统来说存在两大场景即评分预测（rating prediction）与Top-N推荐（item recommendation，item ranking）。评分预测场景主要用于评价网站，比如用户给自己看过的电影评多少分（MovieLens），或者用户给自己看过的书籍评价多少分（Douban）。其中矩阵分解技术主要应用于该场景。Top-N推荐场景主要用于购物网站或者一般拿不到显式评分信息的网站，即通过用户的隐式反馈信息来给用户推荐一个可能感兴趣的列表以供其参考。其中该场景为排序任务，因此需要排序模型来对其建模。因此，我们接下来更关心评分预测任务。

对于评分预测任务来说，我们通常将用户和项目（以电影为例）表示为二维矩阵的形式，其中矩阵中的某个元素表示对应用户对于相应项目的评分，1-5分表示喜欢的程度逐渐增加，？表示没有过评分记录。推荐系统评分预测任务可看做是一个矩阵补全（Matrix Completion）的任务，即基于矩阵中已有的数据（observed data）来填补矩阵中没有产生过记录的元素（unobserved data）。值得注意的是，这个矩阵是非常稀疏的（Sparse），稀疏度一般能达到90%以上，因此如何根据极少的观测数据来较准确的预测未观测数据一直以来都是推荐系统领域的关键问题。

基础背景：SVD 和 FunkSVD

SVD

当然SVD分解的形式为3个矩阵相乘，左右两个矩阵分别表示用户/项目隐含因子矩阵，中间矩阵为奇异值矩阵并且是对角矩阵，每个元素满足非负性，并且逐渐减小。因此我们可以只需要前  个因子来表示它。

如果想运用SVD分解的话，有一个前提是要求矩阵是稠密的，即矩阵里的元素要非空，否则就不能运用SVD分解。很显然我们的任务还不能用SVD，所以一般的做法是先用均值或者其他统计学方法来填充矩阵，然后再运用SVD分解降维。

公式如下

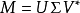
FUNKSVD

SVD首先需要填充矩阵，然后再进行分解降维，同时由于需要求逆操作（复杂度O(n^3)），存在计算复杂度高的问题，所以后来Simon Funk提出了FunkSVD的方法，它不在将矩阵分解为3个矩阵，而是分解为2个低秩的用户项目矩阵，同时降低了计算复杂度：

它借鉴线性回归的思想，通过最小化观察数据的平方来寻求最优的用户和项目的隐含向量表示。同时为了避免过度拟合（Overfitting）观测数据，又提出了带有L2正则项的FunkSVD：

SVD 和 FUNKSVD 的最优化函数都可以通过梯度下降或者随机梯度下降法来寻求最优解。

 PMF:

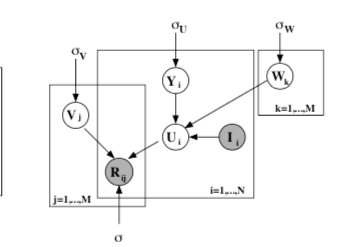
PMF是对于FunkSVD的概率解释版本，它假设评分矩阵中的元素  是由用户潜在偏好向量 和物品潜在属性向量 的内积决定的：

则观测到的评分矩阵条件概率为：

同时，假设用户偏好向量与物品偏好向量服从于均值都为0，方差分别为  ,  的正态分布：

根据贝叶斯公式，可以得出潜变量U,V的后验概率为：

接着，等式两边取对数  后得到：

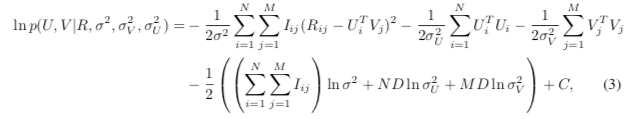
最后，经过推导，我们可以发现PMF确实是FunkSVD的概率解释版本，它两个的形式一样一样的。

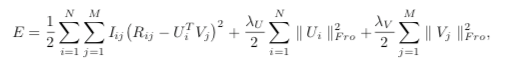
NMF

在普通的SVD的运算过程中，会得到一些负数的embedding，这里，提出了一个假设：分解出来的小矩阵应该满足非负约束。

因为在大部分方法中，原始矩阵  被近似分解为两个低秩矩阵  相乘的形式，这些方法的共同之处是，即使原始矩阵的元素都是非负的，也不能保证分解出的小矩阵都为非负，这就导致了推荐系统中经典的矩阵分解方法可以达到很好的预测性能，但不能做出像User-based CF那样符合人们习惯的推荐解释（即跟你品味相似的人也购买了此商品）。在数学意义上，分解出的结果是正是负都没关系，只要保证还原后的矩阵元素非负并且误差尽可能小即可，但负值元素往往在现实世界中是没有任何意义的。比如图像数据中不可能存在是负数的像素值，因为取值在0~255之间；在统计文档的词频时，负值也是无法进行解释的。因此提出带有非负约束的矩阵分解是对于传统的矩阵分解无法进行科学解释做出的一个尝试。

其中， 分解的两个矩阵中的元素满足非负约束。