【例题收藏】◇例题·III◇ 木と整数 / Integers on a Tree

◇例题·III◇ 木と整数 / Integers on a Tree

只需要一个美妙的转换，这道题就会变得无比美妙……

来源：+AtCoder 2148(ARC-063 E)+

---

◆ 题目大意

给定一棵n个节点（节点被编号为1~n）的树，有K (1≤K≤n) 个节点已经被填上一个数字，现在你需要把剩余的节点填上数字，使得被同一条边相连的两个节点数值相差恰好为1。

若可以实现，先输出一行"Yes"，接下来n行，每行输出一个整数，第i+1行表示节点i的数值；否则输出"No"。

若最初填上的数值没有满足相连两点差为1，也判定为No。

---

◆ 解析

这道题的解法非常美妙~

首先我第一个思路是BFS。一个很简单的结论，每向外延伸一个节点，节点的可取值就会增加2——最大值增加1，最小值减小1。这是很直观的：

于是我储存了每一个节点的可取值范围 [最小值，最大值] ，由于一些点已经给出值，这些点的最大值等于最小值。

另外一个简单结论就是——相邻节点的奇偶性相反（就不证明了）

于是我把已经固定值的节点作为起点：初始化它的最大值、最小值为它的定值；把它push进队列里。

利用BFS，从已知取值范围为[Au,Bu]的点u向外扩展到点v，若v没有确定范围，则v的范围暂时确定为[Au-1,Bu+1]；若已经确定范围为[Av,Bv]，则先判断点v的奇偶性是否冲突（只需要判断最大值或最小值的奇偶性是否冲突就可以了[为什么？想一想就知道了！]），若冲突，则直接输出"No"，否则更新v的范围为[max{Av,Au+1},min{Bv,Au-1}]，若v的取值范围为空（最大值小于最小值），则输出"No"。

最后遍历一遍树，就可以得到所有点的取值了……

唠了这么多……其实这个想法Wa了 QwQ

(肯定被打 @( ◕ x ◕ )@)

下面是正解……

若两点u,v满足v的数值小于u，且u,v之间有满足条件的解，则u到v的路径上的节点的数值存在两种情况：

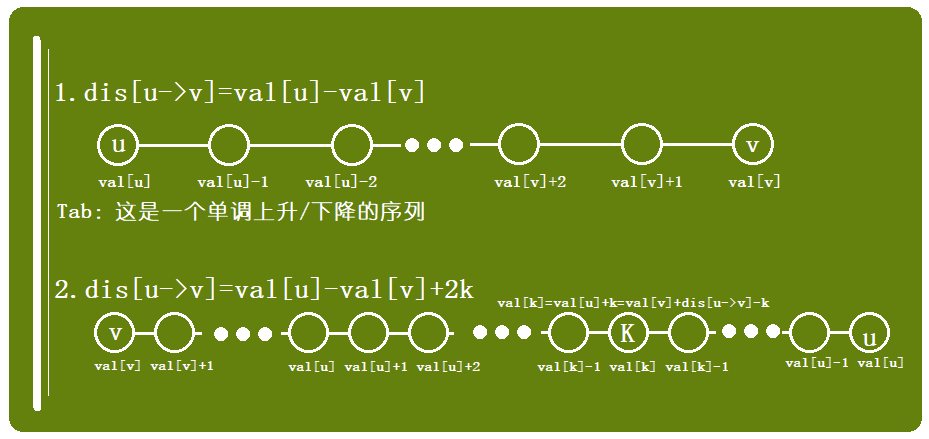
扩展到多个点也是满足的。

如何实现？

定义一个优先队列（小根堆），按节点的数值为关键字排序。我们可以把优先队列的类型定为 pair<int,int> ，因为pair<>的大小关系只取决于第一个元素（.first），所以我们把节点的值作为first，节点编号作为second，就可以实现按数值为关键字排序。同时定义答案数组 ans[]。先把已知节点的答案定为已知值，并push入队列。

每次取出队列的开头，也就是已知值最小且仍可能更新其他节点值的节点。以该节点u为起始点向它相连的点v更新，若ans[v]没有赋值，则直接赋为ans[v]=ans[u]+1；否则判断 |ans[v]-ans[u]| 是否等于1，不满足则输出No。

其他的就请详见代码了~

---

◆ 源代码

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 #include<queue>
 #include<cmath>
 using namespace std;
 const int MAXN=int(1e5),INF=int(1e9);
 vector<int> lnk[MAXN+];
 //邻接表储存图
 priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > que;
 //定义小根堆，first为节点数值，second为节点编号
 int ans[MAXN+];
 //储存已知值
 int n,m;
 int main()
 {
     scanf("%d",&n);
     for(int i=,u,v;i<n;i++)
         scanf("%d%d",&u,&v),
         lnk[u].push_back(v),
         lnk[v].push_back(u);
     scanf("%d",&m);
     fill(ans,ans+MAXN+,INF); //初始化
     for(int i=,x,y;i<m;i++)
         scanf("%d%d",&x,&y),
         que.push(make_pair(y,x)), //将已知节点push进队列
         ans[x]=y;
     while(!que.empty())
     {
         int u=que.top().second,val=que.top().first; //取出已知值最小且可能更新周围节点的节点
         /*什么叫可能更新周围节点？每一次更新一定会更新完一个节点的全部相邻节点，且这些节点不再更新，因此每一个节点在队列里只出现一次*/
         que.pop();
         for(int i=;i<lnk[u].size();i++)
         {
             int v=lnk[u][i];
             if(ans[v]==INF)
                 ans[v]=val+,que.push(make_pair(ans[v],v)); //更新值
             if(fabs(ans[v]-ans[u])!=) //不满足条件
             {
                 printf("No\n");
                 return ;
             }
         }
     }
     printf("Yes\n");
     for(int i=;i<=n;i++)
         printf("%d\n",ans[i]);
     return ;
 }

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）