cf492E. Vanya and Field(扩展欧几里得)

题意

$n \times n$的网格，有$m$个苹果树，选择一个点出发，每次增加一个偏移量$(dx, dy)$，最大化经过的苹果树的数量

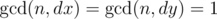
Sol

上面那个互素一开始没看见，然后就GG了

很显然，若$n$和$dx$互素的话，每个$x$都能到达

我们预处理出在每个点$x = 0$时的$y$，取一下最大值即可

求解需要用到扩展欧几里得

/*

*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<vector>
#include<set>
#include<queue>
#include<cmath>
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#define Pair pair<int, int>
#define MP(x, y) make_pair(x, y)
#define fi first
#define se second
#define int long long
#define LL long long
#define ull unsigned long long
#define rg register
#define pt(x) printf("%d ", x);
//#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<22, stdin), p1 == p2) ? EOF : *p1++)
//char buf[(1 << 22)], *p1 = buf, *p2 = buf;
//char obuf[1<<24], *O = obuf;
//void print(int x) {if(x > 9) print(x / 10); *O++ = x % 10 + '0';}
//#define OS  *O++ = ' ';
using namespace std;
//using namespace __gnu_pbds;
const int MAXN = 1e6 + , INF = 1e9 + , mod = 1e9 + ;
const double eps = 1e-;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * f;
}

int N, M, dx, dy, a, b;
int num[MAXN];
int exgcd(int a, int b, int &x, int &y) {
    if(!b) {x = ; y = ; return a;}
    int r = exgcd(b, a % b, x, y);
    int tmp = x; x = y; y = tmp - a / b * y;
    return r;
}
main() {
    N = read(); M = read(); dx = read(); dy = read();
    int ans = ;
    int x, y;
    for(int i = ; i <= M; i++) {
        x = read(), y = read();
        if(x == ) {num[y]++; if(num[y] > num[ans]) ans = y;continue;}
        int r = exgcd(dx, N, a, b);
        a = (a + N) % mod;
        a = (a * x) % N;
    //    a =
        y = (y - a * dy % N + N) % N;
        num[y]++;
        if(num[y] > num[ans]) ans = y;
    }
    printf("%d %d", , ans);

    return ;
}
/*

*/