Zernike不变矩

1、Zernike矩介绍

Zernike矩是基于 Zernike多项式的正交化函数，所利用的正交多项式集是 1个在单位圆内的完备正交集。Zernike矩是复数矩 ,一般把 Zernike矩的模作为特征来描述物体形状。1个目标对象的形状特征可以用 1组很小的 Zernike矩特征向量很好的表示，低阶矩特征向量描述的是 1幅图像目标的整体形状，高阶矩特征向量描述的是图像目标的细节。

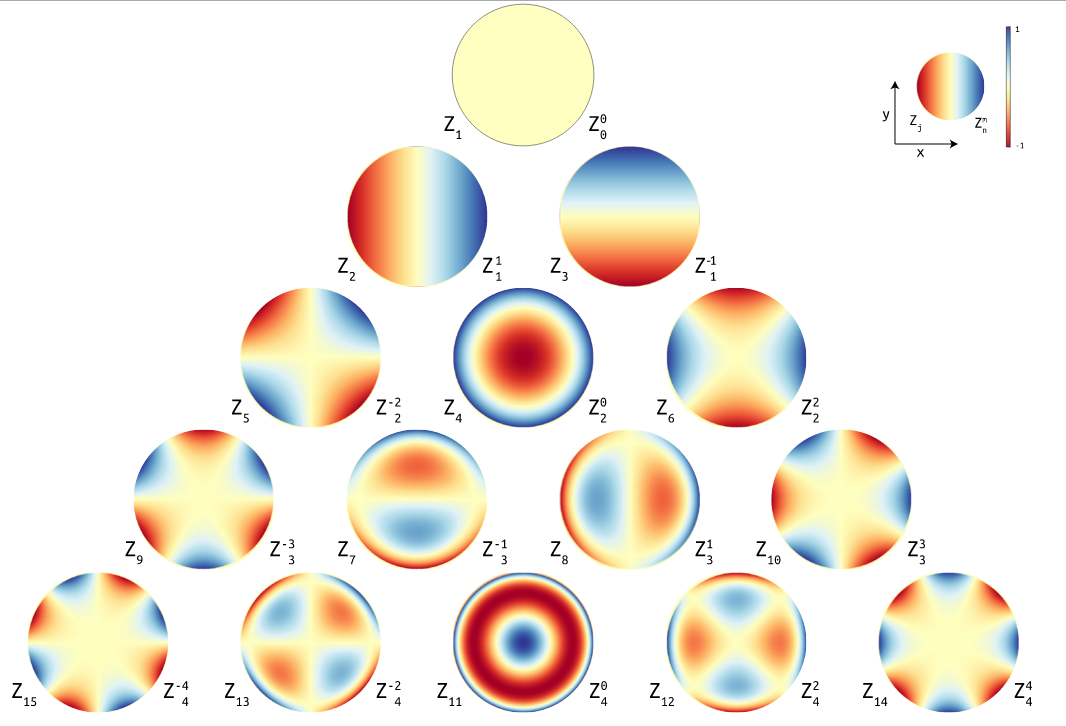
2、Zernike多项式数学描述

Zernike有奇数和偶数之分

若为奇数，则  

若为偶数，则  

其中，

m、n为非负整数，且n>m;

φ 为方位角；

ρ 为半径 ，；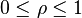

Zernike收敛于[-1,1]之间：；

R_^mn 为径向多项式：

当n-m的值为奇数时，；

当n-m的值为偶数时， R_{^mn =0 。}

3、Zernike的特点

1）当计算 1幅图像的 Zernike矩时 ,以该图像的形心 (也称作重心 )为原点 ,把像素坐标映射到单位圆内。

2）Zernike 矩是一组正交矩,具有旋转不变性的特性,即旋转目标并不改变其模值。

3）低阶矩特征向量描述的是 1幅图像目标的整体形状，高阶矩特征向量描述的是图像目标的细节。

4）通过标准矩来归一化的图像，可以做到平移和尺度不变性。

4、Zernike矩的应用

由于Zernike矩是用来描述图像目标的几何形状信息，所以Zernike图像矩可应用于手势识别、形状识别、图像分类等几何形状明显的特征物。但是不能用来识别丰富的纹理信息的物体。

参考：

维基百科：https://en.wikipedia.org/wiki/Zernike_polynomials

百度百科：http://baike.baidu.com/link?url=_F6XtZkLrUH9lcIyD2MbH8aJhFetRHR29flNItQMciiqktaDRQldo1qjY3LDToKP41XhxJbYJ5D5PP9QKWmdQ_

http://baike.baidu.com/link?url=HVwJi9xDwpq0ABl1FR2wDVp0_R2SGfV8y9OabQGTZA6I85m2ouoiBEjtt9nzDDCccF0lrel5PLLLQtxDx6WTfK

matlab代码：http://www.mathworks.com/matlabcentral/fileexchange/38900-zernike-moments

C代码：http://blog.csdn.net/wrj19860202/article/details/6334275

C++与opencv写的demo：http://download.csdn.net/detail/lengyun_5850/9365199