Luogu P1073 最优贸易

题目描述

C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城市的标号从 1~ n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

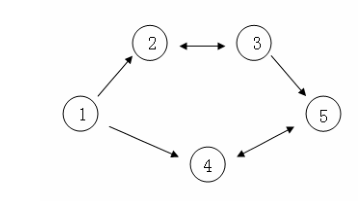
假设 1~n 号城市的水晶球价格分别为 4，3，5，6，1。

阿龙可以选择如下一条线路：1->2->3->5，并在 2 号城市以 3 的价格买入水晶球，在 3号城市以 5 的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路 1->4->5->4->5，并在第 1 次到达 5 号城市时以 1 的价格买入水晶球，在第 2 次到达 4 号城市时以 6 的价格卖出水晶球，赚取的旅费数为 5。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入输出格式

输入格式：

第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 m 行，每行有 3 个正整数，x，y，z，每两个整数之间用一个空格隔开。如果 z=1，表示这条道路是城市 x 到城市 y 之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市y 之间的双向道路。

输出格式：

输出文件 trade.out 共 1 行，包含 1 个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 0。

输入输出样例

输入样例#1：

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2 

输出样例#1：

5

说明

【数据范围】

输入数据保证 1 号城市可以到达 n 号城市。

对于 10%的数据，1≤n≤6。

对于 30%的数据，1≤n≤100。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据，1≤n≤100000，1≤m≤500000，1≤x，y≤n，1≤z≤2，1≤各城市

水晶球价格≤100。

NOIP 2009 提高组 第三题

在做这道题时，犯了很多小错误，打个spfa把vis数组写成了dis，然后一直没发现，但神奇的是样例过了，然后疯狂WA。。。。。。

这道题的思路很简单：

在一条从起点到终点的路上的任意一个点，在这个点的前开后闭区间里买入，并且在前闭后开区见里抛出，最大的差价即为最优贸易

自然想到了spfa但是spfa是依赖边权进行计算的，那怎么办，我们可以把点权赋给相邻的边权。

本题又很多细节需要处理：

1.建图是错综复杂，务必要检查清楚。

2.本图是有环的！判断条件在里面将会将spfa卡住！

3.对于每一次操作（每一条边）都应该在1.该边边权 2.起点值 3.终点值里面筛选min

4.初始化很重要，不然会进入低价的死路！

 #include<bits/stdc++.h>
 using namespace std;
 const int gg=+;
 int n,m;
 int b[+];
 int dis[gg],dis2[gg];
 struct node{
     int w;
     int to;
     int net;
 }a[gg],aa[gg];
 bool vis[gg],vis2[gg];
 int head[gg],head2[gg];
 int cnt,cnt2;

 inline void add2(int i,int j,int w)
 {
     aa[++cnt2].to=j;
     aa[cnt2].net=head2[i];
     aa[cnt2].w=w;
     head2[i]=cnt2;
 }

 inline void add(int i,int j,int w)
 {
     a[++cnt].to=j;
     a[cnt].net=head[i];
     a[cnt].w=w;
     head[i]=cnt;
 }

 inline void spfa(int s)
 {
     deque<int>q;
     for(int i=;i<=n;i++)
     dis[i]=;
     memset(vis,false,sizeof(vis));
     q.push_back(s);
     dis[s]=;
     vis[s]=true;
     while(!q.empty())
     {
         int u=q.front();
         q.pop_front();
         vis[u]=false;
         for(int i=head[u];i;i=a[i].net)
         {
             int v=a[i].to;
             if(dis[v]>min(dis[u],a[i].w))
             {
                 dis[v]=min(dis[u],a[i].w);
                 if(!vis[v])
                 {
                     vis[v]=true;
                     if(q.empty()||dis[v]>dis[q.front()])
                     {
                         q.push_back(v);
                     }
                     else
                     {
                         q.push_front(v);
                     }
                 }
             }
         }
     }
 }

 inline void spfa2(int s)
 {
     deque<int>q;
     for(int i=;i<=n;i++)
     dis2[i]=;
     memset(vis2,false,sizeof(vis2));
     q.push_back(s);
     dis2[s]=;
     vis2[s]=true;
     while(!q.empty())
     {
         int u=q.front();
         q.pop_front();
         vis2[u]=false;
         for(int i=head2[u];i;i=aa[i].net)
         {
             int v=aa[i].to;
             if(dis2[v]<max(dis2[u],aa[i].w))
             {
                 dis2[v]=max(dis2[u],aa[i].w);
                 if(!vis2[v])
                 {
                     vis2[v]=true;
                     if(q.empty()||dis2[v]>dis2[q.front()])
                     {
                         q.push_back(v);
                     }
                     else
                     {
                         q.push_front(v);
                     }
                 }
             }
         }
     }
 }

 int ans=;

 int main()
 {
     cin>>n>>m;
     for(int i=;i<=n;i++)
     {
         cin>>b[i];
     }
     for(int i=;i<=m;i++)
     {
         int q,w,e;
         cin>>q>>w>>e;
         if(e==)
         {
             add(q,w,b[w]);
             add2(w,q,b[q]);
         }
     else if(e==)
         {
             add(q,w,b[w]);
             add(w,q,b[q]);
             add2(q,w,b[w]);
             add2(w,q,b[q]);
         }
     }
     spfa();
     spfa2(n);
     for(int i=;i<=n;i++)
     {
         ans=max(ans,dis2[i]-dis[i]);
     }
     cout<<ans<<endl;
     return ;
 }