基础图像处理之混合空间增强——(Java：拉普拉斯锐化、Sobel边缘检测、均值滤波、伽马变换)
相信看过冈萨雷斯第三版数字图像处理的童鞋都知道，里面涉及到了很多的基础图像处理的算法，今天，就专门借用其中一个混合空间增强的案例，来将常见的几种图像处理算法集合起来，看能发生什么样的化学反应
首先，通过一张图来看下，我们即将需要完成的工作目标
同时，我们也借用书中的人体全身骨骼图像来进行模拟实现这些算法，这样，我们可以通过和书中展示的效果来评判我们实现的算法是否正确，那接下来，我们就来一步一步的实现吧。
第一步：拉普拉斯锐化
这里就不讲解具体的原理了，拉普拉斯是一个二阶微分的算子，这样的算子通过和图像进行卷积操作，可以让我们得到图像中灰度突变区域，就是说那些不同颜色的交界处，下面看代码和运行效果图
public BufferedImage laplaceProcess(BufferedImage src) {
// 拉普拉斯算子
int[] LAPLACE = new int[] { 0, -1, 0, -1, 4, -1, 0, -1, 0 };
int width = src.getWidth();
int height = src.getHeight();
int[] pixels = new int[width * height];
int[] outPixels = new int[width * height];
int type = src.getType();
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
src.getRaster().getDataElements(0, 0, width, height, pixels);
}
src.getRGB(0, 0, width, height, pixels, 0, width);
int k0 = 0, k1 = 0, k2 = 0;
int k3 = 0, k4 = 0, k5 = 0;
int k6 = 0, k7 = 0, k8 = 0;
k0 = LAPLACE[0];
k1 = LAPLACE[1];
k2 = LAPLACE[2];
k3 = LAPLACE[3];
k4 = LAPLACE[4];
k5 = LAPLACE[5];
k6 = LAPLACE[6];
k7 = LAPLACE[7];
k8 = LAPLACE[8];
int offset = 0;
int sr = 0, sg = 0, sb = 0;
int r = 0, g = 0, b = 0;
for (int row = 1; row < height - 1; row++) {
offset = row * width;
for (int col = 1; col < width - 1; col++) {
// red
sr = k0 * ((pixels[offset - width + col - 1] >> 16) & 0xff)
+ k1 * ((pixels[offset - width + col] >> 16) & 0xff)
+ k2
* ((pixels[offset - width + col + 1] >> 16) & 0xff)
+ k3 * ((pixels[offset + col - 1] >> 16) & 0xff) + k4
* ((pixels[offset + col] >> 16) & 0xff) + k5
* ((pixels[offset + col + 1] >> 16) & 0xff) + k6
* ((pixels[offset + width + col - 1] >> 16) & 0xff)
+ k7 * ((pixels[offset + width + col] >> 16) & 0xff)
+ k8
* ((pixels[offset + width + col + 1] >> 16) & 0xff);
// green
sg = k0 * ((pixels[offset - width + col - 1] >> 8) & 0xff) + k1
* ((pixels[offset - width + col] >> 8) & 0xff) + k2
* ((pixels[offset - width + col + 1] >> 8) & 0xff) + k3
* ((pixels[offset + col - 1] >> 8) & 0xff) + k4
* ((pixels[offset + col] >> 8) & 0xff) + k5
* ((pixels[offset + col + 1] >> 8) & 0xff) + k6
* ((pixels[offset + width + col - 1] >> 8) & 0xff) + k7
* ((pixels[offset + width + col] >> 8) & 0xff) + k8
* ((pixels[offset + width + col + 1] >> 8) & 0xff);
// blue
sb = k0 * (pixels[offset - width + col - 1] & 0xff) + k1
* (pixels[offset - width + col] & 0xff) + k2
* (pixels[offset - width + col + 1] & 0xff) + k3
* (pixels[offset + col - 1] & 0xff) + k4
* (pixels[offset + col] & 0xff) + k5
* (pixels[offset + col + 1] & 0xff) + k6
* (pixels[offset + width + col - 1] & 0xff) + k7
* (pixels[offset + width + col] & 0xff) + k8
* (pixels[offset + width + col + 1] & 0xff);
r = sr;
g = sg;
b = sb;
outPixels[offset + col] = (0xff << 24) | (clamp(r) << 16)
| (clamp(g) << 8) | clamp(b);
sr = 0;
sg = 0;
sb = 0;
}
}
BufferedImage dest = new BufferedImage(width, height,
BufferedImage.TYPE_INT_ARGB);
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
dest.getRaster().setDataElements(0, 0, width, height, outPixels);
} else {
dest.setRGB(0, 0, width, height, outPixels, 0, width);
}
return dest;
}
注：左边是原图，右边是运行效果图，由于原图是比较‘缓和’的图片，可以看到拉普拉斯后，生成了一些点，而这些点对应到原图中的位置，正是灰度有突变的地方
紧接着，我们将原图和拉普拉斯锐化后的图进行相加操作，这样，我们就可以看到一样比较清晰的图了，下面是代码和运行效果
/** 拉普拉斯叠加原图像 **/
public BufferedImage laplaceAddProcess(BufferedImage src) { // 拉普拉斯算子
int[] LAPLACE = new int[] { 0, -1, 0, -1, 4, -1, 0, -1, 0 }; int width = src.getWidth();
int height = src.getHeight(); int[] pixels = new int[width * height];
int[] outPixels = new int[width * height]; int type = src.getType();
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
src.getRaster().getDataElements(0, 0, width, height, pixels);
}
src.getRGB(0, 0, width, height, pixels, 0, width); int k0 = 0, k1 = 0, k2 = 0;
int k3 = 0, k4 = 0, k5 = 0;
int k6 = 0, k7 = 0, k8 = 0; k0 = LAPLACE[0];
k1 = LAPLACE[1];
k2 = LAPLACE[2];
k3 = LAPLACE[3];
k4 = LAPLACE[4];
k5 = LAPLACE[5];
k6 = LAPLACE[6];
k7 = LAPLACE[7];
k8 = LAPLACE[8];
int offset = 0; int sr = 0, sg = 0, sb = 0;
int r = 0, g = 0, b = 0;
for (int row = 1; row < height - 1; row++) {
offset = row * width;
for (int col = 1; col < width - 1; col++) { r = (pixels[offset + col] >> 16) & 0xff;
g = (pixels[offset + col] >> 8) & 0xff;
b = (pixels[offset + col]) & 0xff;
// red
sr = k0 * ((pixels[offset - width + col - 1] >> 16) & 0xff)
+ k1 * ((pixels[offset - width + col] >> 16) & 0xff)
+ k2
* ((pixels[offset - width + col + 1] >> 16) & 0xff)
+ k3 * ((pixels[offset + col - 1] >> 16) & 0xff) + k4
* ((pixels[offset + col] >> 16) & 0xff) + k5
* ((pixels[offset + col + 1] >> 16) & 0xff) + k6
* ((pixels[offset + width + col - 1] >> 16) & 0xff)
+ k7 * ((pixels[offset + width + col] >> 16) & 0xff)
+ k8
* ((pixels[offset + width + col + 1] >> 16) & 0xff);
// green
sg = k0 * ((pixels[offset - width + col - 1] >> 8) & 0xff) + k1
* ((pixels[offset - width + col] >> 8) & 0xff) + k2
* ((pixels[offset - width + col + 1] >> 8) & 0xff) + k3
* ((pixels[offset + col - 1] >> 8) & 0xff) + k4
* ((pixels[offset + col] >> 8) & 0xff) + k5
* ((pixels[offset + col + 1] >> 8) & 0xff) + k6
* ((pixels[offset + width + col - 1] >> 8) & 0xff) + k7
* ((pixels[offset + width + col] >> 8) & 0xff) + k8
* ((pixels[offset + width + col + 1] >> 8) & 0xff);
// blue
sb = k0 * (pixels[offset - width + col - 1] & 0xff) + k1
* (pixels[offset - width + col] & 0xff) + k2
* (pixels[offset - width + col + 1] & 0xff) + k3
* (pixels[offset + col - 1] & 0xff) + k4
* (pixels[offset + col] & 0xff) + k5
* (pixels[offset + col + 1] & 0xff) + k6
* (pixels[offset + width + col - 1] & 0xff) + k7
* (pixels[offset + width + col] & 0xff) + k8
* (pixels[offset + width + col + 1] & 0xff);
// 运算后的像素值和原图像素叠加
r += sr;
g += sg;
b += sb;
outPixels[offset + col] = (0xff << 24) | (clamp(r) << 16)
| (clamp(g) << 8) | clamp(b); // next pixel
r = 0;
g = 0;
b = 0;
}
} BufferedImage dest = new BufferedImage(width, height,
BufferedImage.TYPE_INT_ARGB); if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
dest.getRaster().setDataElements(0, 0, width, height, outPixels);
} else {
dest.setRGB(0, 0, width, height, outPixels, 0, width);
}
return dest;
}
同样，左边是原图，右边是原图和经拉普拉斯锐化后相叠加的图，比原图感觉更亮一点了，因为灰度突变的地方加强了
第二步：Sobel提取边缘
接下来，我们还是继续针对原图进行处理，我们想提取原图的边缘，Sobel是一阶算子，结果和图像卷积运算后，可以提取到图像的边缘信息，同样，下面给出代码和运行效果
public BufferedImage sobelProcess(BufferedImage src) {
// Sobel算子
int[] sobel_y = new int[] { -1, -2, -1, 0, 0, 0, 1, 2, 1 };
int[] sobel_x = new int[] { -1, 0, 1, -2, 0, 2, -1, 0, 1 };
int width = src.getWidth();
int height = src.getHeight();
int[] pixels = new int[width * height];
int[] outPixels = new int[width * height];
int type = src.getType();
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
src.getRaster().getDataElements(0, 0, width, height, pixels);
}
src.getRGB(0, 0, width, height, pixels, 0, width);
int offset = 0;
int x0 = sobel_x[0];
int x1 = sobel_x[1];
int x2 = sobel_x[2];
int x3 = sobel_x[3];
int x4 = sobel_x[4];
int x5 = sobel_x[5];
int x6 = sobel_x[6];
int x7 = sobel_x[7];
int x8 = sobel_x[8];
int k0 = sobel_y[0];
int k1 = sobel_y[1];
int k2 = sobel_y[2];
int k3 = sobel_y[3];
int k4 = sobel_y[4];
int k5 = sobel_y[5];
int k6 = sobel_y[6];
int k7 = sobel_y[7];
int k8 = sobel_y[8];
int yr = 0, yg = 0, yb = 0;
int xr = 0, xg = 0, xb = 0;
int r = 0, g = 0, b = 0;
for (int row = 1; row < height - 1; row++) {
offset = row * width;
for (int col = 1; col < width - 1; col++) {
// red
yr = k0 * ((pixels[offset - width + col - 1] >> 16) & 0xff)
+ k1 * ((pixels[offset - width + col] >> 16) & 0xff)
+ k2
* ((pixels[offset - width + col + 1] >> 16) & 0xff)
+ k3 * ((pixels[offset + col - 1] >> 16) & 0xff) + k4
* ((pixels[offset + col] >> 16) & 0xff) + k5
* ((pixels[offset + col + 1] >> 16) & 0xff) + k6
* ((pixels[offset + width + col - 1] >> 16) & 0xff)
+ k7 * ((pixels[offset + width + col] >> 16) & 0xff)
+ k8
* ((pixels[offset + width + col + 1] >> 16) & 0xff);
xr = x0 * ((pixels[offset - width + col - 1] >> 16) & 0xff)
+ x1 * ((pixels[offset - width + col] >> 16) & 0xff)
+ x2
* ((pixels[offset - width + col + 1] >> 16) & 0xff)
+ x3 * ((pixels[offset + col - 1] >> 16) & 0xff) + x4
* ((pixels[offset + col] >> 16) & 0xff) + x5
* ((pixels[offset + col + 1] >> 16) & 0xff) + x6
* ((pixels[offset + width + col - 1] >> 16) & 0xff)
+ x7 * ((pixels[offset + width + col] >> 16) & 0xff)
+ x8
* ((pixels[offset + width + col + 1] >> 16) & 0xff);
// green
yg = k0 * ((pixels[offset - width + col - 1] >> 8) & 0xff) + k1
* ((pixels[offset - width + col] >> 8) & 0xff) + k2
* ((pixels[offset - width + col + 1] >> 8) & 0xff) + k3
* ((pixels[offset + col - 1] >> 8) & 0xff) + k4
* ((pixels[offset + col] >> 8) & 0xff) + k5
* ((pixels[offset + col + 1] >> 8) & 0xff) + k6
* ((pixels[offset + width + col - 1] >> 8) & 0xff) + k7
* ((pixels[offset + width + col] >> 8) & 0xff) + k8
* ((pixels[offset + width + col + 1] >> 8) & 0xff);
xg = x0 * ((pixels[offset - width + col - 1] >> 8) & 0xff) + x1
* ((pixels[offset - width + col] >> 8) & 0xff) + x2
* ((pixels[offset - width + col + 1] >> 8) & 0xff) + x3
* ((pixels[offset + col - 1] >> 8) & 0xff) + x4
* ((pixels[offset + col] >> 8) & 0xff) + x5
* ((pixels[offset + col + 1] >> 8) & 0xff) + x6
* ((pixels[offset + width + col - 1] >> 8) & 0xff) + x7
* ((pixels[offset + width + col] >> 8) & 0xff) + x8
* ((pixels[offset + width + col + 1] >> 8) & 0xff);
// blue
yb = k0 * (pixels[offset - width + col - 1] & 0xff) + k1
* (pixels[offset - width + col] & 0xff) + k2
* (pixels[offset - width + col + 1] & 0xff) + k3
* (pixels[offset + col - 1] & 0xff) + k4
* (pixels[offset + col] & 0xff) + k5
* (pixels[offset + col + 1] & 0xff) + k6
* (pixels[offset + width + col - 1] & 0xff) + k7
* (pixels[offset + width + col] & 0xff) + k8
* (pixels[offset + width + col + 1] & 0xff);
xb = x0 * (pixels[offset - width + col - 1] & 0xff) + x1
* (pixels[offset - width + col] & 0xff) + x2
* (pixels[offset - width + col + 1] & 0xff) + x3
* (pixels[offset + col - 1] & 0xff) + x4
* (pixels[offset + col] & 0xff) + x5
* (pixels[offset + col + 1] & 0xff) + x6
* (pixels[offset + width + col - 1] & 0xff) + x7
* (pixels[offset + width + col] & 0xff) + x8
* (pixels[offset + width + col + 1] & 0xff);
// 索贝尔梯度
r = (int) Math.sqrt(yr * yr + xr * xr);
g = (int) Math.sqrt(yg * yg + xg * xg);
b = (int) Math.sqrt(yb * yb + xb * xb);
outPixels[offset + col] = (0xff << 24) | (clamp(r) << 16)
| (clamp(g) << 8) | clamp(b);
}
}
BufferedImage dest = new BufferedImage(width, height,
BufferedImage.TYPE_INT_ARGB);
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
dest.getRaster().setDataElements(0, 0, width, height, outPixels);
} else {
dest.setRGB(0, 0, width, height, outPixels, 0, width);
}
return dest;
}
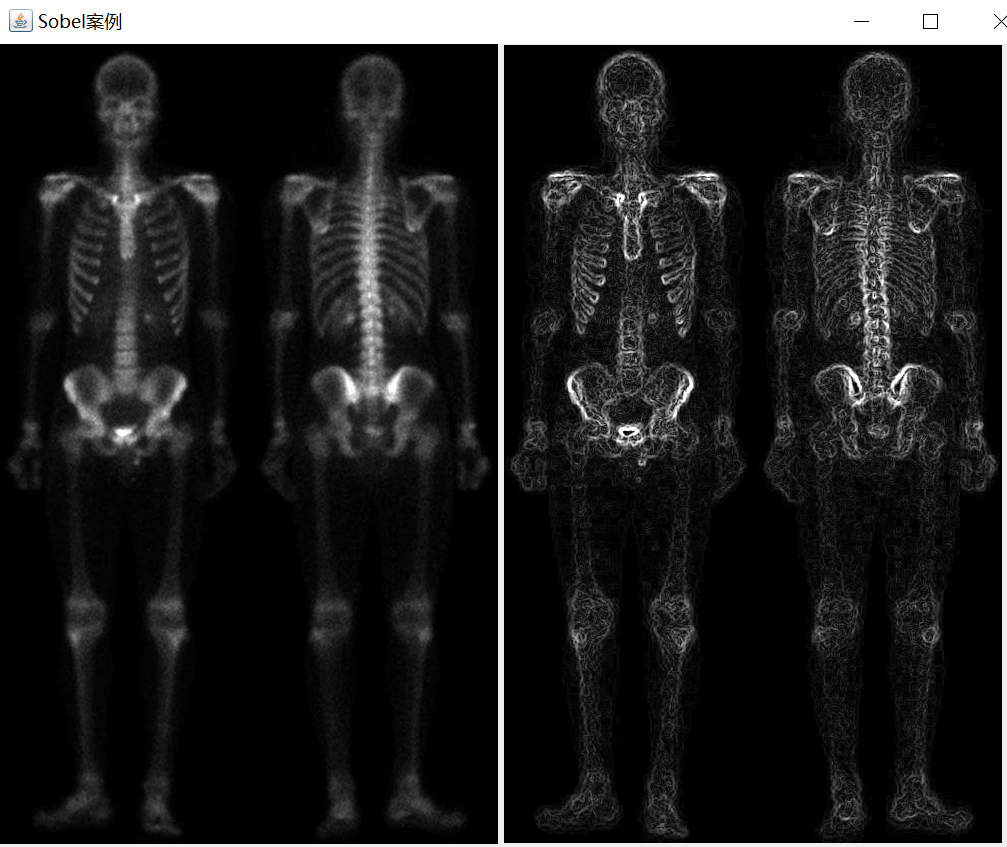
注：左边是原图，右边是经过Sobel变换后的图，从图中可以明显看到Sobel达到的效果
第三步：均值滤波
这一步需要在Sobel变换后得到的图像基础上进行进一步的变换，均值滤波，就是将图像中每一点的像素值用其周边多个像素值的平均值重新赋值，有3*3，5*5的滤波器，我们即将使用的是5*5的滤波器，即是说，将某一个像素点重新赋值为以其为中心的25的像素值的平均值，下面我们看下代码和运行效果
/** 均值滤波 **/
public BufferedImage meanValueProcess(BufferedImage src) { BufferedImage image = this.sobelProcess(src);// 已经索贝尔处理的图像 int width = image.getWidth();
int height = image.getHeight(); int[] pixels = new int[width * height];
int[] outPixels = new int[width * height]; int type = image.getType();
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
image.getRaster().getDataElements(0, 0, width, height, pixels);
}
image.getRGB(0, 0, width, height, pixels, 0, width); // 均值滤波使用的卷积模板半径，这里使用5*5均值，所以半径使用2
int radius = 2;
int total = (2 * radius + 1) * (2 * radius + 1); int r = 0, g = 0, b = 0;
for (int row = 0; row < height; row++) {
for (int col = 0; col < width; col++) {
int sum = 0;
for (int i = -radius; i <= radius; i++) {
int roffset = row + i;
roffset = (roffset < 0) ? 0
: (roffset >= height ? height - 1 : roffset); for (int j = -radius; j <= radius; j++) { int coffset = col + j;
coffset = (coffset < 0) ? 0
: (coffset >= width ? width - 1 : coffset); int pixel = pixels[roffset * width + coffset]; r = (pixel >> 16) & 0XFF; sum += r;
}
} r = sum / total;
g = sum / total;
b = sum / total; outPixels[row * width + col] = (255 << 24) | (clamp(r) << 16)
| (clamp(g) << 8) | clamp(b);
}
} BufferedImage dest = new BufferedImage(width, height,
BufferedImage.TYPE_INT_ARGB); if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
dest.getRaster().setDataElements(0, 0, width, height, outPixels);
} else {
dest.setRGB(0, 0, width, height, outPixels, 0, width);
} return dest;
}
注：左边是原图，右边是经Sobel变换后再经5*5均值滤波变换的效果，我们可以看到，均值滤波有模糊的效果
第四步：数学变换
在进行伽马变换之前，我们需要将经拉普拉斯锐化后的图像和经Sobel及均值滤波后得到的图像进行相乘，此外，还要和原图进行相加，经过这些数学变化后的图像，再进行伽马变化，下面先给出这些数学变化的代码和效果图
/** 数学运算*/
public BufferedImage mathProcess(BufferedImage src) { // 获取经拉普拉斯运算后与原图叠加的图片
BufferedImage lapsImage = this.laplaceAddProcess(src); // 获取索贝尔5*5均值滤波后的图像
BufferedImage meanImage = this.meanValueProcess(src); int type = src.getType();
int width = src.getWidth();
int height = src.getHeight(); // 原始图像的像素信息
int[] pixels = new int[width * height];
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
src.getRaster().getDataElements(0, 0, width, height, pixels);
}
src.getRGB(0, 0, width, height, pixels, 0, width); // 拉普拉斯锐化后的像素信息
int[] lapsPixels = new int[width * height];
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
lapsImage.getRaster().getDataElements(0, 0, width, height,
lapsPixels);
}
lapsImage.getRGB(0, 0, width, height, lapsPixels, 0, width); // Sobel和均值滤波后的像素信息
int[] meanPixels = new int[width * height];
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
meanImage.getRaster().getDataElements(0, 0, width, height,
meanPixels);
}
meanImage.getRGB(0, 0, width, height, meanPixels, 0, width); int[] outPixels = new int[width * height]; // 图像相乘
int lr = 0, lg = 0, lb = 0;
int mr = 0, mg = 0, mb = 0;
int or = 0, og = 0, ob = 0;
int r = 0, g = 0, b = 0;
for (int row = 0; row < height; row++) {
for (int col = 0; col < width; col++) {
int lpixel = lapsPixels[row * width + col];
int mpixel = meanPixels[row * width + col]; // 原始图像
int opixel = pixels[row * width + col]; lr = (lpixel >> 16) & 0XFF;
mr = (mpixel >> 16) & 0XFF;
or = (opixel >> 16) & 0XFF; lg = (lpixel >> 8) & 0XFF;
mg = (mpixel >> 8) & 0XFF;
og = (opixel >> 8) & 0XFF; lb = (lpixel) & 0XFF;
mb = (mpixel) & 0XFF;
ob = (opixel) & 0XFF; /** 图像相乘 标定到0~255 */
r = (lr * mr) / 255;
g = (lg * mg) / 255;
b = (lb * mb) / 255; // 相乘后图像与原图相加
r = r + or;
g = g + og;
b = b + ob; outPixels[row * width + col] = (255 << 24) | (clamp(r) << 16)
| (clamp(g) << 8) | (clamp(b));
}
} BufferedImage dest = new BufferedImage(width, height,
BufferedImage.TYPE_INT_ARGB); if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
dest.getRaster().setDataElements(0, 0, width, height, outPixels);
} else {
dest.setRGB(0, 0, width, height, outPixels, 0, width);
} return dest;
} private int clamp(int value) {
return value > 255 ? 255 : (value < 0 ? 0 : value);
}
注：左边是原图，右边是将经过拉普拉斯锐化的图像和经过Sobel及均值滤波后的图像相乘再和原图像叠加的效果
第四步：伽马变换
伽马变换也叫幂律变换，是一个幂函数，可以压缩和扩展灰度级，图像经过幂函数的处理后，增加了对比度，下面看下代码和运行效果图，也是最终的效果图
/** 伽马变化 */
public BufferedImage gammaProcess(BufferedImage src) { BufferedImage image = this.mathProcess(src); double gamma = 0.5;// 幂级数 int type = image.getType();
int width = src.getWidth();
int height = src.getHeight(); // 经过数学变换后的像素信息
int[] pixels = new int[width * height];
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
image.getRaster().getDataElements(0, 0, width, height, pixels);
}
image.getRGB(0, 0, width, height, pixels, 0, width); int[] outPixels = new int[width * height]; // 建立LUT查找表
int[] lut = new int[256];
for (int i = 0; i < 256; i++) { float f = (float) (i / 255.0);
f = (float) Math.pow(f, gamma); lut[i] = (int) (f * 255.0);
} int r = 0, g = 0, b = 0;
int or = 0, og = 0, ob = 0;
for (int row = 0; row < height; row++) {
for (int col = 0; col < width; col++) { int pixel = pixels[row * width + col]; r = (pixel >> 16) & 0XFF;
g = (pixel >> 8) & 0XFF;
b = (pixel) & 0XFF; or = lut[r];
og = lut[g];
ob = lut[b]; outPixels[row * width + col] = (255 << 24) | (clamp(or) << 16)
| (clamp(og) << 8) | (clamp(ob)); }
} BufferedImage dest = new BufferedImage(width, height,
BufferedImage.TYPE_INT_ARGB);
if (type == BufferedImage.TYPE_INT_ARGB
|| type == BufferedImage.TYPE_INT_RGB) {
dest.getRaster().setDataElements(0, 0, width, height, outPixels);
} else {
dest.setRGB(0, 0, width, height, outPixels, 0, width);
} return dest;
}
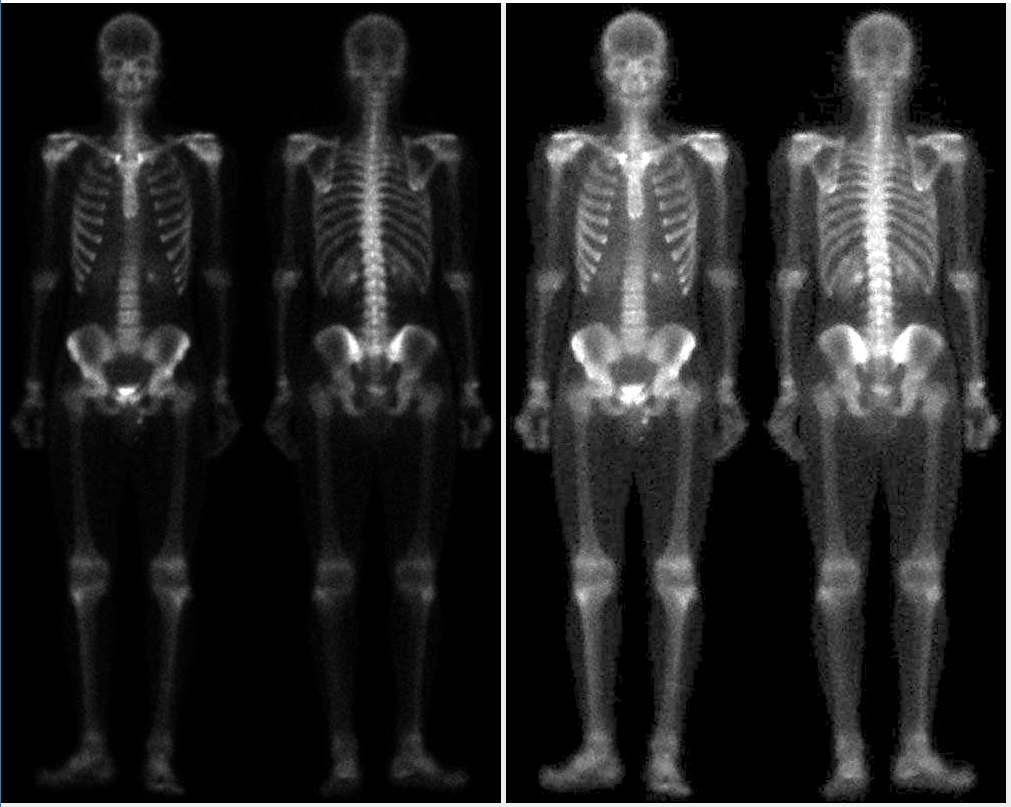
注：左边是原图，右边是最终效果图，经过伽马变换，扩展了灰度级，可以展示出人体的整个轮廓
这样，一个完成的案例就完成了，每一步的实现效果也都和书中的插图是一样的，如果有错误的地方欢迎指正！
基础图像处理之混合空间增强——(Java：拉普拉斯锐化、Sobel边缘检测、均值滤波、伽马变换)的更多相关文章
- 图像增强算法（直方图均衡化、拉普拉斯、Log、伽马变换）
一.图像增强算法原理 图像增强算法常见于对图像的亮度.对比度.饱和度.色调等进行调节,增加其清晰度,减少噪点等.图像增强往往经过多个算法的组合,完成上述功能,比如图像去燥等同于低通滤波器,增加清晰度则 ...
- C++数字图像处理（1）-伽马变换
https://blog.csdn.net/huqiang_823/article/details/80767019 1.算法原理 伽马变换(幂律变换)是常用的灰度变换,是一种简单的图像增强算法 ...
- 对比度增强（二）：直方图正规划与伽马变换 cv.normal（）函数使用及原理
直方图正规化: 图像为I,宽为W,高为H,I(r,c)代表I的第r行第c列的灰度值:输出图像记为O,为使得输出图像的灰度值在[Omin,Omax]范围里,可用如下公式: ...
- Atitti 图像处理 图像混合 图像叠加 blend 原理与实现
Atitti 图像处理 图像混合 图像叠加 blend 原理与实现 混合模式 编辑 本词条缺少信息栏,补充相关内容使词条更完整,还能快速升级,赶紧来编辑吧! 混合模式是图像处理技术中的一个技术名词,不 ...
- Matlab图像处理系列2———空间域平滑滤波器
注:本系列来自于图像处理课程实验,用Matlab实现最主要的图像处理算法 本文章是Matlab图像处理系列的第二篇文章.介绍了空间域图像处理最主要的概念----模版和滤波器,给出了均值滤波起和中值滤波 ...
- JVM基础系列第6讲：Java 虚拟机内存结构
看到这里,我相信大家对于一个 Java 源文件是如何变成字节码文件,以及字节码文件的含义已经非常清楚了.那么接下来就是让 Java 虚拟机运行字节码文件,从而得出我们最终想要的结果了.在这个过程中,J ...
- JVM基础系列第2讲：Java 虚拟机的历史
说起 Java 虚拟机,许多人就会将其与 HotSpot 虚拟机等同看待.但实际上 Java 虚拟机除了 HotSpot 之外,还有 Sun Classic VM.Exact VM.BEA JRock ...
- JVM基础系列第1讲：Java 语言的前世今生
Java 语言是一门存在了 20 多年的语言,其年纪比我自己还大.虽然存在了这么长时间,但 Java 至今都是最大的工业级语言,许多大型互联网公司均采用 Java 来实现其业务系统.大到国际电商巨头阿 ...
- Java基础学习总结（80）——Java性能优化详解
让Java应用程序运行是一回事,但让他们跑得快就是另外一回事了.在面对对象的环境中,性能问题就像来势凶猛的野兽.但JVM的复杂性将性能调整的复杂程度增加了一个级别.这里Refcard涵盖了JVM in ...
随机推荐
- 【Alpha】功能规格说明书
更新说明:从用户需求分析中剥离有关用户场景分析部分,加入功能规格说明书. Github地址:https://github.com/buaase/Phylab-Web/blob/master/docs/ ...
- 《Linux内核分析》第一周学习小结 计算机是如何工作的？
<Linux内核分析>第一周.计算机是如何工作的? 20135204 郝智宇 一.存储程序计算机工作模型 1. 冯诺依曼体系结构: 数字计算机的数制采用二进制:计算机应该按照程 ...
- LINUX基础实验报告
实验一:主要是介绍Linux系统概况,无运行代码. 实验二:Linux的基本操作 重要知识点 [Tab] 使用Tab键来进行命令补全,Tab键一般键盘是在字母Q旁边,这个技巧给你带来的最大的好处就是当 ...
- C++：多态浅析
1.多态 在C++中由两种多态性: • 编译时的多态性:通过函数的重载和运算符的重载来实现的 • 运行时的多态性:通过类继承关系和虚函数来实现的 特别注意: a.运行时的多态性是指程序执行前,无法根据 ...
- 贝叶斯先验解释l1正则和l2正则区别
这里讨论机器学习中L1正则和L2正则的区别. 在线性回归中我们最终的loss function如下: 那么如果我们为w增加一个高斯先验,假设这个先验分布是协方差为 的零均值高斯先验.我们在进行最大似然 ...
- Jmeter使用笔记之函数
用Jmeter才做了一个项目的测试,就不得不对函数这部分吐槽一下,真是有点弱,难怪大多数人不用这个功能,不过如果用的好也是很方便的,以下慢慢说. 一.BeanShell函数 在测试中遇到了时间戳的加减 ...
- Linux命令（三） 移动文件 mv
用户可以使用 mv 命令来移动文件或目录至另一个文件或目录, 还可以将目录或文件重命名. 如果将一个文件移动到一个已经存在的目标文件中,目标文件的内容将会被覆盖.mv 命令接收两个参数时,第一个参数表 ...
- k8s kubectl edit 方式修改 nodeport 的端口
0. 买了一本 每天五分钟玩转 k8s 还有 刚才转帖的blog 里面有一个 kubectl edit 的语法能够在线更改端口号 ,之前一直没弄明白. 刚才做了下实验.发现很好用 这里记录一下. 1. ...
- day5——Java 实现导出excel表 POI（转）
1.首先下载poi-3.6-20091214.jar,下载地址如下: http://download.csdn.net/detail/evangel_z/3895051 2.Student.java ...
- browser-sync & http server
browser-sync & http server browser-sync https://www.browsersync.io/ usage # step 1 $ npm install ...