Windows命令-系统木马取样
1、前言
工作中偶尔会遇到去现场提取木马样本回公司分析的情况。如果是生产环境下,不方便安装各类抓包、安全软件时。能用系统自带的命令去定位出木马程序相关的信息是最理想不过的状态。
2、Windows常用命令
2.1 查询端口
netstat -an // -a 显示所有连接和侦听端口 -n 以数字形式显示地址和端口号。
2.2 查询进程
netstat -anb // 查询端口对应的进程名 -b 显示在创建每个连接或侦听端口时涉及的可执行程序。注:需要特别注意权限问题,没有足够的权限数据显示不全
wmic process list // 查询进程名对应的系统路径
2.3 查询连接网络的域名
开启 dnscache缓存服务,运行以下命令后,域名记录在dnsrslvr.log内。
net stop dnscache
type nul > %systemroot%\system32\dnsrsvlr.log
type nul > %systemroot%\system32\dnsrslvr.log
type nul > %systemroot%\system32\asyncreg.log
cacls %systemroot%\system32\dnsrsvlr.log /E /G "NETWORK SERVICE":W
cacls %systemroot%\system32\dnsrslvr.log /E /G "NETWORK SERVICE":W
cacls %systemroot%\system32\asyncreg.log /E /G "NETWORK SERVICE":W
net start dnscache
3、效果
通过Malware Defender可以抓取到进程访问的IP,通过Windows的DNS记录则可以看到对应的域名。测试环境是Windows 7 x86环境
3.1 Malware Defender

3.2 Windows的DNS记录
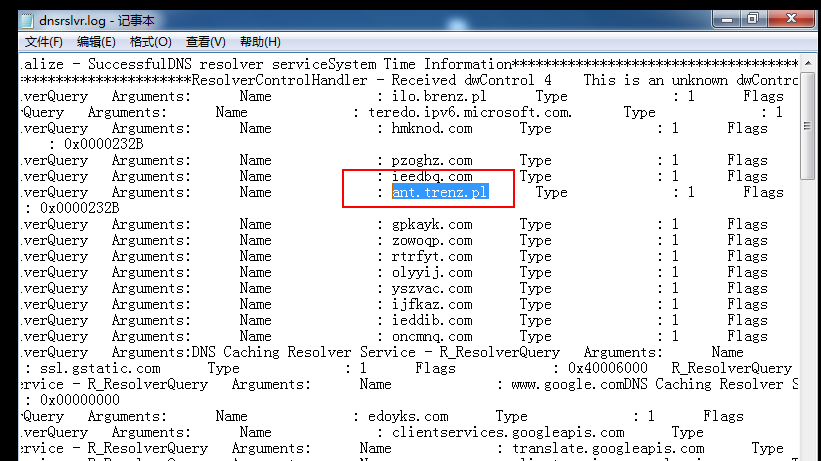

Windows命令-系统木马取样的更多相关文章
- Mac OSX系统、Linux、Windows命令行教程
目录 Mac OSX系统.Linux.Windows命令行教程 一.各系统终端的使用方法 二.各系统命令的功能 Mac OSX系统.Linux.Windows命令行教程 用你的终端做一些事情 (com ...
- Powershell 命令行安装 Windows 作业系统
使用 powershell 完全安装或重灌 windows 作业系统的正确姿势 note:完全使用 powershell 指令,绝非在 powershell 终端下键入传统的 cmd 指令使用传统的 ...
- 命令查询windows&Linux系统版本信息
Linux 查询系统名字输入"cat /proc/version",说明正在运行的内核版本uname -rwindows 查询系统名字win+r -> winversyste ...
- windows命令行工具
winver 检查Windows版本 wmimgmt.msc 打开Windows管理体系结构(wmi) wupdmgr Windows更新程序 wscript Windows脚本宿主设置 write ...
- windows命令大全(转载)
winver---------检查Windows版本 wmimgmt.msc打开Windows管理体系结构(wmi) wupdmgrWindows更新程序 w脚本Windows脚本宿主设置 write ...
- windows命令
开始--运行--cmd 进入命令提示符 输入netstat -ano 即可看到所有连接的PID 之后在任务管理器中找到这个PID所对应的程序如果任务管理器中没有PID这一项,可以在任务管理器中选&qu ...
- Windows 7系统下删除开机引导项的方法
Windows 7系统下删除开机引导项的方法: 1.使用管理员权限运行cmd,在命令行窗口使用 bcdedit 回车 2.查找description为你想删除的段,看对应的标识符是多少, 然后使用 ...
- Windows命令行中使用SSH连接Linux
转自 http://www.linuxidc.com/Linux/2014-02/96625.htm 1.下载: openssh for Winodws: 免费下载地址在 http://linux.l ...
- 【转】G40-70、G50-70联想小新笔记本SR1000随机Linux改Windows 7系统操作指导
http://support1.lenovo.com.cn/lenovo/wsi/htmls/detail_20140505150749705.html 适用范围:G40-70,G50-70联想小新笔 ...
随机推荐
- someday团队Postmortem(事后诸葛亮会议)
一.会议相关介绍: 时间:2018年1月12日 地点:第九实验楼五楼机房 参会人员:someday团队全体成员 二.每个成员在beta阶段的实践和alpha阶段有何改进? (一)设想和目标: 我们的软 ...
- 读C#程序最小公倍数答案就是:2123581660200
阅读下面程序,请回答如下问题: 问题1:这个程序要找的是符合什么条件的数? 问题2:这样的数存在么?符合这一条件的最小的数是什么? 问题3:在电脑上运行这一程序,你估计多长时间才能输出第一个结果?时间 ...
- springmvc下载文件
Controller内代码: @RequestMapping(value = "/upload") public ResponseEntity<byte[]> uplo ...
- Docker的安装和使用说明——Docker for Windows
一.Docker安装 1.1官方方法 官方下载页面:http://www.docker.com/products/docker#/windows 官方下载地址:https://download.doc ...
- 从苦逼到牛逼,详解Linux运维工程师的打怪升级之路
做运维也快四年多了,就像游戏打怪升级,升级后知识体系和运维体系也相对变化挺大,学习了很多新的知识点. 运维工程师是从一个呆逼进化为苦逼再成长为牛逼的过程,前提在于你要能忍能干能拼,还要具有敏锐的嗅觉感 ...
- Android 图表
今天在群里有人提问Android的图表,在网上搜索了一下,在贴吧中看到的回答,说是Trinea整理的开源项目,不知道是不是博客上的Trinea. 将内容记录如下,以备需要时查看. GraphView ...
- USACO 2012 December ZQUOJ 24122 Scrambled Letters(二分)
题意:有一个字典序名单,现在把这些名单的顺序和名字的字符顺序扰乱了,要输出原先的名字在原来的名单中的最低和最高位置. 分析:先将所有的名字串按字典序从小到大和从大到小分别排序smin[]和smax[] ...
- 导入appiumlibrary显红
1.点击ride中的Tools的View RIDE Log 2.打开日志报如下错误,提示没有six这个模块,可能是最新包的要对python版本兼容 3.所以使用pip install six安装包后 ...
- 在配置文件里面设置bean 那么在类里面就要提供set方法用以注入
在配置文件里面设置bean 那么在类里面就要提供set方法用以注入
- [JZOJ 5402] God Knows
终于搞完了这乡里别题目 $ $ 考虑一个 \(dp\) ,设 \(f[i]\) 表示最后一个匹配选 \((i,p[i])\) 的最小费用 首先我们考虑答案长什么样 假设根据 \(p[i]\) 排序 , ...
