因子分析(Factor analysis)

1.引言

在高斯混合和EM算法中，我们运用EM算法拟合混合模型，但是我们得考虑得需要多少的样本数据才能准确识别出数据中的多个高斯模型！看下面两种情况的分析：

• 第一种情况假如有 m 个样本，每个样本的维度是 n, 如果 n » m, 这时哪怕拟合出一个高斯模型都很困难，更不用说高斯混合, 为什么呢?

这和解多元线性方程组是一样的道理，就是自变量的个数多于非线性相关的方程的个数，这必然导致解的不唯一，虽然在解方程的时候可以随便选一个解满足方程组，但是对于某一实际数据集，往往样本对应的概率分布在客观上都是唯一的，只是我们无法简单地用概率论中的几个典型的分布准确表示出来罢了！

• 另一种情况是 m 个样本的维度都较低，用高斯分布对数据建模，用最大似然估计去估计均值（期望）和方差：

我们会发现，协方差矩阵 Σ 是奇异的，即 Σ 不可逆，Σ^-1 不存在，且 但是这两项在计算多元高斯分布时，又都是必不可少的。

所以，除非 m 比 n 大一定较合适的数值，否则对方差和均值的最大似然估计将会很难找到正确的值。

然而，我们仍然能够拟合出关于数据的合理的高斯分布，并且或许还能挖掘出数据的一些有趣的变化结构。如何做到的呢？

---

 2.对 Σ 的约束

如果没有充足的数据拟合出完全的协方差矩阵，就要对协方差矩阵的空间作出一些限制。

• 例如，我们要拟合出一个协方差矩阵使得该矩阵为对角矩阵，在最大似然估计中，对角协方差矩阵满足：

• 有时，要限制这个对角矩阵的元素必须相等，即，其中 I 是单位矩阵，是可以调整元素大小的参数，可以推导出：

如果拟合数据的一个无约束的，非稀疏的协方差矩阵，为了保证最大似然估计得出的协方差矩阵Σ 非奇异，必须要求 m ≥ n+1.

但是，要求 Σ 是对角矩阵就意味着所有数据样本的坐标是独立且非相关的（具体原因回顾概率论有关协方差的知识，参考机器学习中有关概率论知识的小结），

通常情况下，如果能捕获出数据中内在的一些感兴趣的相关结构就更好了！如果按照上述的两种约束，做不到这一点。

后面会介绍一种因子分析模型(factor analysis model), 将会使用更多参数而不仅仅是协方差矩阵Σ，捕获出数据中的一些关联，同时不用必须拟合一个全协方差矩阵.

---

3.高斯分布的边缘分布和条件分布

在讨论因子分析模型之前，先回顾下概率论中的一些知识，就是如何求出多元高斯分布的条件分布和边缘分布。

• 假设一个向量随见变量：

其中即 x₁, x₂ 都是向量.

• 假设 其中：

其中 等等。注意由于协方差矩阵式对称矩阵，所以

在我们的假设下，x₁, x₂ 服从多元高斯分布，那么什么是x₁ 的边缘分布呢？

容易看出，

关于 x 的协方差，即 x₁, x₂ 的联合协方差：

可以看出左上角的分块是与我们计算的 x₁ 的协方差相一致。

由于高斯分布的边缘分布还是高斯分布，于是 x₁ 的边缘分（把x₂ 看成是常量）布写作

那什么是在给定 x₂ 时，x₁ 的条件分布呢？通常被写为：，其中：

在讨论因此分析模型的时候，这些计算边缘分布和条件分布的式子将会很有用。

---

4.因子分析模型

在因子分析模型中，假设一个关于联合分布，其中是隐变量：

模型中的参数 μ 是向量：，矩阵，矩阵，k 的取值通常比 n 小.

因此，可以把每一个数据点  看作是从一个 k 维的多元高斯分布  采样得到的.

可以把上面的因子模型假设等效写成下面的形式（这种等效的意义和目的请看本文最后的总结）：

其中和相互独立。

下面看看我们模型到底定义出了什么样的分布。

由上面的式子可以看出，我们的随机变量 z 和 x 服从联合高斯分布 ：

现在来找出和.

由上面的条件知道：，所以：

注意上面推理中 矩阵 Λ 不是随机变量，里面的所有元素都是常量，所以 Λ 的期望仍是本身。

因此可以得出：

　　

为了得出，需要计算：

由于，所以

在对后一步中，

同样有：

综上所述有：

因此的边缘分布：

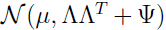
给定一个训练集，那么参数的的对数似然函数为：

对这个似然函数最大化看上去就很麻烦，确实也很麻烦，但是有稍微简单点的方法，那就是EM算法（EM算法参考EM算法原理详解）

---

5.EM算法运用于因子分析

• E步：计算 

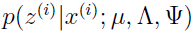
把上面式子（3）的结果代入式子（1）（2），得到：

有这两个参数，即数学期望和协方差，可以写出要求的条件高斯分布：

• M步：需要最大化上面分布的关于参数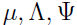的对数似然函数：

这里以如何优化参数为例详解，首先把上面的式子简化为：

下标表示是服从分布.

因为现在要优化参数，所以把与无关的项去掉，因为无关项此时就是常数，没有优化的必要，只需与参数有关的项最大化即可，而我们需要最大化：

可以发现只有最后一项与参数有关，利用（注意 tr 是线性代数中的“迹”）：

可以得到关于的偏导：

令这个偏导数为0，可以得到：

解出参数：

由的定义知道是一个均值为，方差为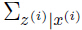的高斯分布，很容易得到：

注意后面的一个等式是如何得到的：对于一个随机变量因此

把上面连个等式的结果代入式子（7），可以得到：

类似地，我们可以优化参数和：

• 

• 

令，即只取矩阵对角线上的元素.

---

6.总结

在因子分析模型的讨论中可以发现，因子分析模型就是一种降维的概率模型。可以这么想：

• 要对数据 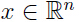进行建模，而由于维度太高，即 n 太大，处理起来很棘手，那么就想办法对 x 进行线性变换，映射到一个较低维的空间，维度设为 k, k 要远远小于 n, 设每一个数据点在 k 维空间中对应的数据点是 ，由上面讨论可知 数据 z 服从高斯分布，且维度较低，就以高斯分布建模很方便。
• 但是 z 毕竟不是我们要建模的数据，于是通过在通过高斯采样得到 之后，运用进行线性变换(严格来说叫做仿射变换，这里为了容易理解)，将数据 z 由 k 维空间映射到 n 维空间，由于原始数据常常存在噪声，所以我们同样假设了噪声也服从高斯分布，即，所以就得到了原始数据
• 因为每一个都是由相应的经过变换，再加上噪声得来，所以是关于的后验分布，即一开始模型假设中的：

　　　这样建模就避免直接处理高维数据，而是先建模较低维数据，然后通过一定的简单的映射，加上噪声就很容易得出原始数据分布参数，即期望和协方差，且模型假设原始数据服从 　　 高斯分布，所以这个分布就和容易写出来，然后通过高斯采样就可以得到原始数据的非常近似的数据了。