CRT && exCRT模板

CRT从各种方面上都吊打exCRT啊......

短，好理解...

考虑构造bi使得bi % pi = ai，bi % pj = 0。然后全加起来就行了。

显然bi的构造就是ai * (P/pi) * inv(P/pi)。

LL a = , p = MO - ;
for(int i = ; i <= ; i++) {
    a = (a + ans[i] * (p / mod[i]) % p * qpow(p / mod[i], mod[i] - , mod[i]) % p) % p;
}

exCRT：

是这样的，重新手推了一个短一点的模板。题是洛谷P3868 猜数字

 inline int exCRT(int n, int *a, int *b) {
     int t = a[], p = b[], x, y;
     for(int i = ; i <= n; i++) {
         int g = exgcd(p, b[i], x, y);
         p = lcm(p, b[i]);
         t = (t - a[i]) % p;
         y = y * (t / g) % p;
         t = (a[i] + y * b[i]) % p;
     }
     return t;
 }

具体操作的时候开long long，龟速乘，记得全程避免负数。

---

先背为敬。

 #include <cstdio>
 #include <algorithm>

 typedef long long LL;
 const int N = ;

 LL p[N], a[N];

 inline LL mod(LL a, LL c) {
     if(c < ) {
         c = (~c) + ;
     }
     while(a >= c) {
         a -= c;
     }
     while(a < ) {
         a += c;
     }
     return a;
 }
 inline LL mul(LL a, LL b, LL c) {
     LL ans = ;
     while(b) {
         if(b & ) {
             ans = mod(ans + a, c);
         }
         a = mod(a << , c);
         b = b >> ;
     }
     return ans;
 }
 LL exgcd(LL a, LL b, LL &x, LL &y) {
     if(!b) {
         x = ;
         y = ;
         return a;
     }
     LL g = exgcd(b, a % b, x, y);
     std::swap(x, y);
     y -= (a / b) * x;
     return g;
 }

 int main() {
     int n;
     scanf("%d", &n);
     for(int i = ; i <= n; i++) {
         scanf("%lld%lld", &p[i], &a[i]);
     }

     LL A = a[], P = p[];
     for(int i = ; i <= n; i++) {
         LL x, y;
         LL C = (a[i] - A), g = exgcd(P, p[i], x, y);
         C = (C % p[i] + p[i]) % p[i];
         if(C % g) {
             puts("-1");
             return ;
         }

         x = mul(x, C / g, P / g * p[i]);
         A += mul(x, P, P / g * p[i]);
         P *= p[i] / g;
         A = mod(A, P);
     }

     // x === A mod P
     LL x, y;
     exgcd(P, , y, x);
     x *= A;
     x = (x % P + P) % P;
     printf("%lld\n", x);
     return ;
 }

AC代码

尝试合并两个同余方程：

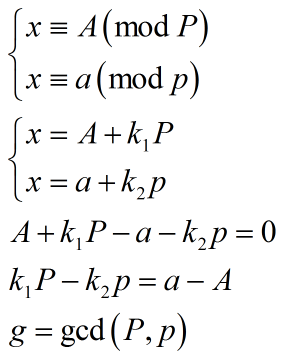
判断有解后可用exgcd解方程。

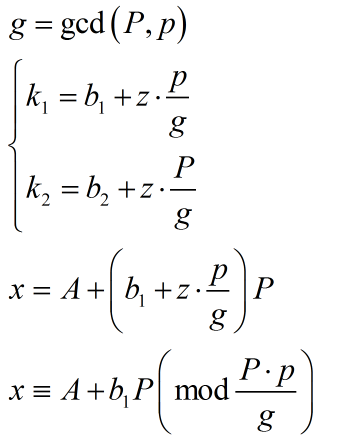
至此合并完成。

所有方程逐一合并即可。