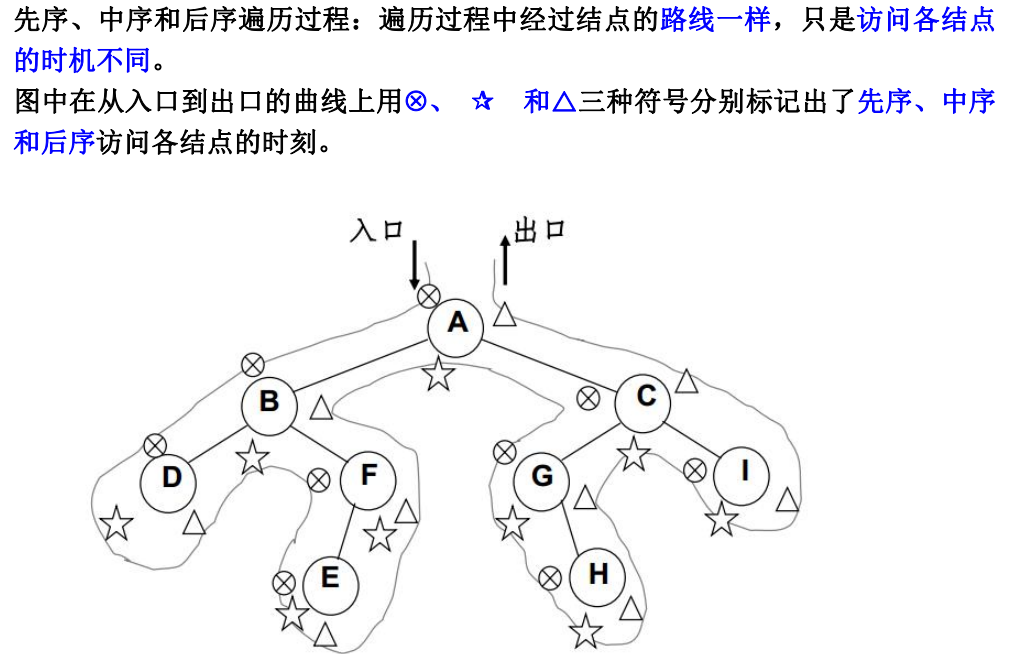
树的遍历c/c++

先序遍历（递归）

1 void preOrderTraverase(TreeNode * r)
2 {
3     if(r)
4     {
5         printf("%d\t",r->_data);
6         preOrderTraverase(r->_left);
7         preOrderTraverase(r->_right);
8     }
9 }                

中序遍历（递归）

1 void midOrderTraverase(TreeNode * r)
2 {
3     if(r)
4     {
5         midOrderTraverase(r->_left);
6         printf("%d\t",r->_data);
7         midOrderTraverase(r->_right);
8     }
9 }    

后序遍历（递归）

1 void postOrderTraverase(TreeNode * r)
2 {
3     if(r)
4     {
5         postOrderTraverase(r->_left);
6         postOrderTraverase(r->_right);
7         printf("%d\t",r->_data);
8     }
9 }

层序遍历（用到队列）（递归）

 1 void levelOrderTraverse(TreeNode *root)
 2 {
 3     if(root)
 4     {
 5         Queue q;
 6         initQueue(&q);
 7         enQueue(&q,root);
 8         while(!isQueueEmpty(&q))
 9         {
10             root = deQueue(&q);                    //根出队
11             printf(" %d ",root->data);
12             if(root->left)enQueue(&q,root->left); //左子树入队
13             if(root->right)enQueue(&q,root->right);//右子树入队
14         }
15         printf("\n");
16     }
17 }

先序遍历（非递归）

 1 void preOrderTraverase(TreeNode * r)
 2 {
 3     if(r)
 4     {
 5         Stack s;
 6         initStack(&s);
 7         while(r || !isStackEmpty(&s)) //第一次循环或者栈内不空
 8         {
 9             while(r)
10             {
11                 printf("%d\t",r->_data);//访问结点
12                 push(&s,r);
13                 r = r->_left;          //一直向左并将沿途结点压入堆栈
14             }
15             if(!isStackEmpty(&s))
16             {
17                 r = pop(&s);          //结点弹出堆栈
18                 r = r->_right;        //转向右子树
19             }
20         }
21     }
22 }                    

中序遍历（非递归）

 1 void midOrderTraverase(TreeNode * r)
 2 {
 3     if(r)
 4     {
 5         Stack s;
 6         initStack(&s);
 7         while(r || !isStackEmpty(&s))
 8         {
 9             while(r)
10             {
11                 push(&s,r);
12                 r = r->_left;
13             }
14             if(!isStackEmpty(&s))
15             {
16                 r = pop(&s);
17                 printf("%d\t",r->_data);//访问的时机变了
18                 r = r->_right;
19             }
20         }
21     }
22 }    

后序遍历（非递归）

 

对于任一节点 P，

1.将节点 P 入栈；

2.若 P 不存在左孩子和右孩子，或者 P 存在左孩子或右孩子，但左右孩子已经被输出，

则可以直接输出节点 P，并将其出栈，将出栈节点 P 标记为上一个输出的节点，再将此时的栈顶结点设为当前节点；

3.若不满足2中的条件，

则将 P 的右孩子和左孩子依次入栈，当前节点重新置为栈顶结点，之后重复操作2；

4.直到栈空，遍历结束。

 1 void postOrderTraverse(struct Tree *t)
 2 {
 3     Stack s; initStack(&s);
 4     TreeNode *cur;          //当前结点
 5     TreeNode *pre=NULL; //前一次访问的结点
 6     push(&s,t);
 7     while(!isStackEmpty(&s))
 8     {
 9         cur = pop(&s);
10         push(&s,cur);
11         if((cur->_left==NULL&&cur->_right==NULL)|| (pre!=NULL&&(pre==cur->_left||pre==cur->_right)))
12         { //如果当前结点没有孩子结点或者孩子节点都已被访问过
13             printf("%d\t",cur->_data);
14             pop(&s);
15             pre=cur;
16         }
17         else
18         {
19             if(cur->_right != NULL)
20                 push(&s,cur->_right);
21             if(cur->_left != NULL)
22                 push(&s,cur->_left);
23         }
24     }
25 }